练习册

  • 练习册
  • 试题
    相关习题
     0  231206  231214  231220  231224  231230  231232  231236  231242  231244  231250  231256  231260  231262  231266  231272  231274  231280  231284  231286  231290  231292  231296  231298  231300  231301  231302  231304  231305  231306  231308  231310  231314  231316  231320  231322  231326  231332  231334  231340  231344  231346  231350  231356  231362  231364  231370  231374  231376  231382  231386  231392  231400  266669 

    科目： 来源： 题型：选择题

    4．若直线y=x-b与曲线$\left\{\begin{array}{l}{x=2+cosθ}\\{y=sinθ}\end{array}\right.$（θ∈[0，2π]）有两个不同的公共点，则实数b的取值范围为（　　）
    A．（2-$\sqrt{2}$，1）B．[2-$\sqrt{2}$，2+$\sqrt{2}$]C．（-∞，2-$\sqrt{2}$）∪（2+$\sqrt{2}$，+∞）D．（2-$\sqrt{2}$，2+$\sqrt{2}$）

    查看答案和解析>>

    科目： 来源： 题型：解答题

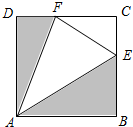    3．一位创业青年租用了一块边长为1百米的正方形田地ABCD来养蜂、产蜜与售蜜，他在正方形的边BC，CD上分别取点E，F（不与正方形的顶点重合），连接AE，EF，FA，使得∠EAF=45°．现拟将图中阴影部分规划为蜂源植物生长区，△AEF部分规划为蜂巢区，△CEF部分规划为蜂蜜交易区．若蜂源植物生长区的投入约为2×105元/百米2，蜂巢区与蜂蜜交易区的投入约为105元/百米2，则这三个区域的总投入最少需要多少元？

    查看答案和解析>>

    科目： 来源： 题型：解答题

    2．已知函数f（x）=|x-4|+a|x+2|（a∈R）的图象关于点（1，0）中心对称．
    （1）求实数a的值；
    （2）解不等式f（x）≥3．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    1．已知x、y满足$\frac{{x}^{2}}{3}$+y2=1，则u=|2x+y-4|+|3-x-2y|的取值范围为（　　）
    A．[1，12]B．[0，6]C．[0，12]D．[1，13]

    查看答案和解析>>

    科目： 来源： 题型：解答题

    20．设函数f（x）=lnx-ax2-$\frac{1}{2}$x．
    （Ⅰ） 当a=$\frac{1}{4}$时，求f（x）的最大值；
    （Ⅱ） 令g（x）=f（x）+ax2+$\frac{1}{2}$x+$\frac{a}{x}$，x∈（0，3]，其图象上任意一点P（x0，y0）处的切线的斜率k≤$\frac{1}{2}$恒成立，求实数a的取值范围；
    （Ⅲ） 当a=0时，方程2mf（x）=x（x-3m）有唯一实数解，求正实数m的值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    19．已知函数f（x）=ax2-lnx（a∈R）
    （1）当a=1时，求曲线y=f（x）在点（1，f（1））的切线方程；
    （2）若?x∈（0，1]，|f（x）|≥1恒成立，求a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．在平面直角坐标系xOy中，已知曲线C：$\left\{\begin{array}{l}x=6cosα\\ y=3sinα\end{array}$（α为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．
    （Ⅰ）求曲线C的极坐标方程；
    （Ⅱ）若点A，B为曲线C上的两点，且OA⊥OB，求|OA|•|OB|的最小值．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    17．若函数f（x）=lnx-x-mx在区间[1，e2]内有唯一的零点，则实数m的取值范围是[-1，$\frac{2}{{e}^{2}}$-1）∪{$\frac{1}{e}$-1}．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．在对人们休闲方式的一次调查中，共调查120人，其中女性70人、男性50人，女性中有40人主要的休闲方式是看电视，另外30人主要的休闲方式是运动；男性中有20人主要的休闲方式是看电视，另外30人主要的休闲方式是运动．
    （Ⅰ）根据以上数据建立一个2×2的列联表；
    （Ⅱ）在犯错误的概率不超过0.10的前提下，认为休闲方式与性别是否有关？
    参考数据：独立性检验临界值表
    p（K2≥k0） 0.500.400.250.150.100.050.0250.0100.0050.001
    k00.4550.7081.3232.0722.7063.8415.0246.6357.87910.828
    K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，n=a+b+c+d．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    15．已知函数f（x）=ax-1-lnx．（a∈R）
    （Ⅰ）讨论函数f（x）的单调性；
    （Ⅱ）若函数f（x）在x=2处的切线斜率为$\frac{1}{2}$，不等式f（x）≥bx-2对任意x∈（0，+∞）恒成立，求实数b的取值范围；
    （Ⅲ）证明对于任意n∈N，n≥2有：$\frac{{ln{2^2}}}{2^2}$+$\frac{{ln{3^2}}}{3^2}$+$\frac{{ln{4^2}}}{4^2}$+…+$\frac{{ln{n^2}}}{n^2}$＜$\frac{{2{n^2}-n-1}}{2（n+1）}$．

    查看答案和解析>>

    同步练习册答案