4．设关于x的方程k•9^x-k•3^x+1+6（k-5）=0在[0，2]内有解，求k的取值范围．

3．过点P（2，1）作圆x²+y²=1的两条切线PA，PB，其中A、B为切点，求直线AB方程．

2．广播电台为了了解某地区的听众对某个戏曲节目的收听情况，随机抽取了100名听众进行调查，下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图，将日均收听该节目时间不低于40分钟的听众成为“戏迷”
（Ⅰ）根据已知条件完成2×2列联表，并判断“戏迷”与性别是否有关？

	“戏迷”	非戏迷	总计
男
女	10		55
总计

附：K²=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$，

P（K2≥k）	0.05	0.01
k	3.841	6.635

（Ⅱ）将上述调查所得到的频率当作概率．现在从该地区大量的听众中，采用随机抽样的方法每次抽取1名听众，抽取3次，记被抽取的3名听众中“戏迷”的人数为X，若每次抽取的结果相互独立，求X的分布列，数学期望及方差．

1．已知a为实数，函数f（x）=alnx+x²-4x
（1）当a=1时，求函数f（x）在x=1处的切线方程；
（2）设g（x）=（a-2）x，若?x∈[$\frac{1}{e}$，e]，使得f（x）≥g（x）成立，求实数a的取值范围．
（3）定义：若函数m（x）的图象上存在两点A、B，设线段AB的中点为P（x₀，y₀），若m（x）在点Q（x₀，m（x₀））处的切线l与直线AB平行或重合，则函数m（x）是“中值平均函数”，切线l叫做函数m（x）的“中值平均切线”．试判断函数f（x）是否是“中值平均函数”？若是，判断函数f（x）的“中值平均切线”的条数；若不是，说明理由．

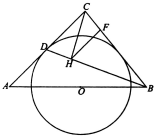20．如图，等腰直角三角形ACB中，∠ACB=90°，圆心O为AB的中点，AC切圆O于点D．
（I）证明：BC为圆O的切线；
（Ⅱ）连接BD，作CH⊥DB，H为垂足，作HF⊥BC，F为垂足，求$\frac{BF}{DH}$的值．

19．圆C经过直线x+y-1=0与x²+y²=4的交点，且圆C的圆心为（-2，-2），则过点（2，4）向圆C作切线，所得切线方程为x=2和5x-12y+38=0．

18．如图，PA与圆O相切于点A，割线PO与圆O交于C，D两点，DE垂直直径AB于E，且2OE=OB=1，则PC等于1．

17．如图，圆O与等腰直角三角形ABC的两直角边相切，交斜边BC于F，G两点，且BF=FG=$\sqrt{2}$，则圆O的半径等于1．

16．直线y=kx+2k与圆（x-1）²+y²=4相交于M，N两点，若|MN|≤2，则k的取值范围是（　　）

A．

[-$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{2}}{2}$]

B．

（-∞，-$\frac{\sqrt{2}}{2}$]∪[$\frac{\sqrt{2}}{2}$，+∞）

C．

[-$\frac{2\sqrt{5}}{5}$，-$\frac{\sqrt{2}}{2}$]∪[$\frac{\sqrt{2}}{2}$，$\frac{2\sqrt{5}}{5}$]

D．

（-$\frac{2\sqrt{5}}{5}$，-$\frac{\sqrt{2}}{2}$]∪[$\frac{\sqrt{2}}{2}$，$\frac{2\sqrt{5}}{5}$）

15．已知点A（1，1），B（1，3），圆C：（x-a）²+（y+a-2）²=4上存在点P，使得PB²-PA²=32，则圆心横坐标a的取值范围为[7，9]．