练习册

  • 练习册
  • 试题
    相关习题
     0  231325  231333  231339  231343  231349  231351  231355  231361  231363  231369  231375  231379  231381  231385  231391  231393  231399  231403  231405  231409  231411  231415  231417  231419  231420  231421  231423  231424  231425  231427  231429  231433  231435  231439  231441  231445  231451  231453  231459  231463  231465  231469  231475  231481  231483  231489  231493  231495  231501  231505  231511  231519  266669 

    科目： 来源： 题型：解答题

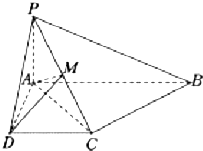    20．如图，已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，且∠DAB=90°，∠ABC=45°，CB=$\sqrt{2}$，AB=2，PA=1．
    （1）求证：BC⊥平面PAC；
    （2）若M是PC的中点，求二面角M-AD-C的大小．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    19．有甲乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如表的列联表．
     优秀非优秀总计
    甲班10  
    乙班 30 
    合计  100
    已知在全部100人中抽到随机抽取1人为优秀的概率为$\frac{3}{10}$
    （1）请完成如表的列联表；
    （2）根据列联表的数据，有多大的把握认为“成绩与班级有关系“？
    （3）按分层抽样的方法，从优秀学生中抽出6名学生组成一个样本，再从样本中抽出2名学生，记甲班被抽到的人数为ξ，求ξ的分布列和数学期望．
    参考公式和数据：K2=$\frac{n（ad-bc）^{2}}{（a+c）（b+d）（a+b）（c+d）}$，其中n=a+b+c+d
    下面的临界值表供参考：
    p（K2≥k0）0.150.100.050.0250.0100.0050.001
    k02.0722.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．已知：如图，在Rt△ABC中∠ACB=90°，CD⊥AB，E为AC的中点．ED、CB延长线交于一点F．求证：AC•DF=BC•CF．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    17．2+22+23…+25n-1+a被31除所得的余数为3，则a的值为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．如图，已知四棱锥S-ABCD的底面ABCD是正方形，SA⊥底面ABCD，E是SC上的一点．
    （1）求证：平面EBD⊥平面SAC；
    （2）设SA=4，AB=2，求点A到平面SBD的距离；
    （3）若AB=2，求当SA的值为多少时，二面角B-SC-D的大小为120°．并说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

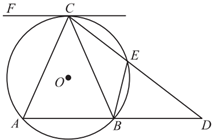    15．如图，已知CF是圆O的切线，C为切点，弦AB∥CF，E为圆周上一点，CE交AB的延长线于点D，弧$\widehat{AB}$=弧$\widehat{BC}$．求证：
    （1）△ABC是等边三角形；
    （2）△BCE∽△BCD．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    14．如图所示，梯形ABCD中，AD∥BC，它的两条对角线交于O，若S△AOD：S△ACD=1：4，则S△AOD：S△BOC=1：9．

    查看答案和解析>>

    科目： 来源： 题型：解答题

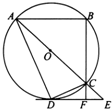    13．如图，AC是⊙O的直径，ABCD是圆内接四边形，DE与⊙O相切于点D，AC的延长线交DE于点E，BC的延长线交DE于点F，且AB∥DE．
    （Ⅰ）求证：CD平分∠ACF．
    （Ⅱ）若AB=3EF，⊙O的半径为1，求线段DE的长．

    查看答案和解析>>

    科目： 来源： 题型：解答题

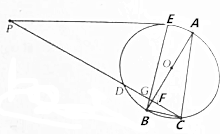    12．如图所示，已知圆O的一条直径为AB，PE是圆O的一条切线，E为切点，PC是圆O的一条割线，且交圆O于C，D两点，AB交PC于F，BE交PC于G，△AFC∽△ACB．
    （1）求证：∠PEG=∠PGE；
    （2）若PG=5，PD=3，求DC的长度．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    11．斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形，侧棱AA1长为$\frac{3}{2}$a，它和AB、AC均为60°，斜三棱柱的全面积 为$\frac{3+4\sqrt{3}}{2}{a}^{2}$．

    查看答案和解析>>

    同步练习册答案