
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | ($\frac{5}{e}$,2] | B. | [$\frac{5}{2e}$,2) | C. | (-$\frac{1}{2}$,-$\frac{5}{2e}$] | D. | [-2,-$\frac{5}{2e}$) |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
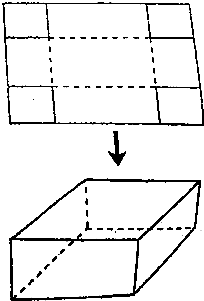 用长为16cm,宽为10cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四周的四个小矩形向上翻转90°角,再焊接而成(如图),问该容器的高x为多少时,容器的容积V(x)最大?最大容积是多少?
用长为16cm,宽为10cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四周的四个小矩形向上翻转90°角,再焊接而成(如图),问该容器的高x为多少时,容器的容积V(x)最大?最大容积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com