练习册

  • 练习册
  • 试题
    相关习题
     0  231355  231363  231369  231373  231379  231381  231385  231391  231393  231399  231405  231409  231411  231415  231421  231423  231429  231433  231435  231439  231441  231445  231447  231449  231450  231451  231453  231454  231455  231457  231459  231463  231465  231469  231471  231475  231481  231483  231489  231493  231495  231499  231505  231511  231513  231519  231523  231525  231531  231535  231541  231549  266669 

    科目： 来源： 题型：填空题

    17．不等式|2x-1|-|x+2|＞0的解集为$（-∞，-\frac{1}{3}）∪（3，+∞）$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．用总长为10.8m的钢条制作一个长方体容器的框架，如果所制容器底面一边的长是另一边的长的2倍，那么高为多少时容器的容积最大？最大容积是多少？

    查看答案和解析>>

    科目： 来源： 题型：解答题

    15．某商场销售某种品牌的空调器，每周周初购进一定数量的空调器，商场每销售一台空调器可获利500元，若供大于求，则每台多余的空调器需交保管费100元；若供不应求，则可从其他商店调剂供应，此时每台空调器仅获利润200元．
    （Ⅰ）若该商场周初购进20台空调器，求当周的利润（单位：元）关于当周需求量n（单位：台，n∈N）的函数解析式f（n）；
    （Ⅱ）该商场记录了去年夏天（共10周）空调器需求量n（单位：台），整理得表：
    周需求量n1819202122
    频数12331
    以10周记录的各需求量的频率作为各需求量发生的概率，若商场周初购进20台空调器，X表示当周的利润（单位：元），求X的分布列及数学期望．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    14．已知函数f（x）=|x-a|+4x，a＞0．
    （Ⅰ）当a=2时，求不等式f（x）≥2x+1的解集；
    （Ⅱ）若x∈（-2，+∞）时，恒有f（2x）≥7x+a2-3，求实数a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    13．在平面直角坐标系xOy中，动点P到定点F（0，-1）的距离与P到定直线y=-2的距离的比为$\frac{\sqrt{2}}{2}$，动点P的轨迹记为C．
    （1）求轨迹C的方程；
    （2）若点M在轨迹C上运动，点N在圆E：x2+（y-0.5）2=r2（r＞0）上运动，且总有|MN|≥0.5，
    求r的取值范围；
    （3）过点Q（-$\frac{1}{3}$，0）的动直线l交轨迹C于A、B两点，试问：在此坐标平面上是否存在一个定点T，使得无论l如何转动，以AB为直径的圆恒过点T？若存在，求出点T的坐标．若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    12．某制造商制造并出售球型瓶装的某种饮料．瓶子的制造成本是0.8πr2分，其中r是瓶子的半径，单位是厘米．已知每出售1mL的饮料，制造商可获利0.2分，且制造商能制作的瓶子的最大半径为6cm．问题：
    （1）瓶子的半径多大时，能使每瓶饮料的利润最大？
    （2）瓶子的半径多大时，每瓶的利润最小？

    查看答案和解析>>

    科目： 来源： 题型：解答题

    11．已知函数f（x）=|x-a|．
    （Ⅰ）若不等式f（x）≤6的解集为{x|-4≤x≤8}，求实数a的值；
    （Ⅱ）在（1）的条件下，对任意实数x都有f（x）≥m-f（-x）恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

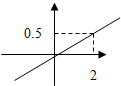    10．某商场欲经销某种商品，考虑到不同顾客的喜好，决定同时销售A，B两个品牌，根据生产厂家营销策略，结合本地区以往经销该商品的数据统计分析，A品牌的销售利润y1与投入资金x成正比，其关系如图所示，B品牌的销售利润y2与投入资金x的关系为y2=$\frac{3}{4}\sqrt{x}$．
    （1）求A品牌的销售利润y1与投入资金x的函数关系式．
    （2）该商场计划投入5万元经销该种商品中，并全部投入A，B两个品牌，问：怎样分配这5万元资金，才能使经销该种商品获得最大利润，其最大利润为多少万元？

    查看答案和解析>>

    科目： 来源： 题型：解答题

    9．某电视生产厂家有A、B两种型号的电视机参加家电下乡活动．若厂家投放A、B型号电视机的价值分别为p、q万元，农民购买电视机获得的补贴分别为$\frac{2}{5}$lnp、$\frac{1}{10}$q万元．已知厂家对A、B两种型号电视机的投放总金额为10万元，且A、B两型号的电视机投放金额都不低于1万元，请你制定一个投放方案，使得在这次活动中农民得到的补贴最多，并求出其最大值（精确到0.1，参考数据：ln4≈1.4）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    8．如图，E是圆内两弦AB和CD的交点，直线EF∥CB，交AD的延长线于F，FG切圆于G．求证：
    （1）△DFE∽△EFA；
    （2）EF=FG．

    查看答案和解析>>

    同步练习册答案