
科目: 来源: 题型:解答题
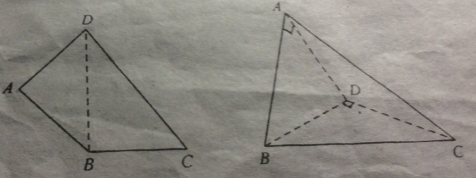
 已知正三棱锥S-ABC底面边长为2$\sqrt{3}$,过侧棱SA与底面中心O作截面SAD,在△SAD中,若SA=AD,求侧面与底面所成二面角的余弦值.
已知正三棱锥S-ABC底面边长为2$\sqrt{3}$,过侧棱SA与底面中心O作截面SAD,在△SAD中,若SA=AD,求侧面与底面所成二面角的余弦值.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | -9M | B. | 9M | C. | 27M | D. | -27M |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
 设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q,点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$.
设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q,点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$.查看答案和解析>>
科目: 来源: 题型:解答题
 如图所示,△ABC与△DBC是边长均为2的等边三角形,且所在两平面互相垂直,EA⊥平面ABC,且EA=$\sqrt{3}$.
如图所示,△ABC与△DBC是边长均为2的等边三角形,且所在两平面互相垂直,EA⊥平面ABC,且EA=$\sqrt{3}$.查看答案和解析>>
科目: 来源: 题型:填空题
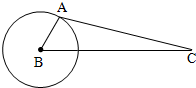 通讯卫星C在赤道上空3R(R为地球半径)的轨道上,它每24小时绕地球一周,所以它定位于赤道上某一点的上空.如果此点与某地A(北纬60°)在同一条子午在线,则在A观察此卫星的仰角的正切值为$\frac{3}{6}$.
通讯卫星C在赤道上空3R(R为地球半径)的轨道上,它每24小时绕地球一周,所以它定位于赤道上某一点的上空.如果此点与某地A(北纬60°)在同一条子午在线,则在A观察此卫星的仰角的正切值为$\frac{3}{6}$.查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com