练习册

  • 练习册
  • 试题
    相关习题
     0  231456  231464  231470  231474  231480  231482  231486  231492  231494  231500  231506  231510  231512  231516  231522  231524  231530  231534  231536  231540  231542  231546  231548  231550  231551  231552  231554  231555  231556  231558  231560  231564  231566  231570  231572  231576  231582  231584  231590  231594  231596  231600  231606  231612  231614  231620  231624  231626  231632  231636  231642  231650  266669 

    科目： 来源： 题型：选择题

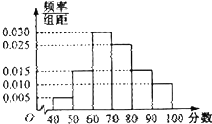    8．某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分成6组：加以统计，得到如图所示的频率分布直方图．已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为（　　）
    A．588B．480C．450D．120

    查看答案和解析>>

    科目： 来源： 题型：选择题

    7．已知y=f（x）是定义在R上的奇函数，且f（x）=$\left\{\begin{array}{l}{（x+2）^{2}-1，x＜-1}\\{0，-1≤x≤0}\end{array}\right.$，当函数y=f（x-1）-$\frac{1}{2}$-k（x-2）（其中k＞0）的零点个数取得最大值时，则实数k的数值范围是（　　）
    A．（0，6-$\sqrt{30}$）B．（6-$\sqrt{30}$，2$-\sqrt{2}$）C．（$\frac{1}{4}$，6-$\sqrt{30}$）D．（$\frac{1}{4}$，2-$\sqrt{2}$）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    6．已知函数f（x）=e3x-1，g（x）=ln（1+2x）+ax，f（x）的图象在x=$\frac{1}{3}$处的切线与g（x）的图象也相切．
    （1）求a的值；
    （2）当x＞-$\frac{1}{2}$时，求证：f（x）＞g（x）；
    （3）设p，q，r∈（-$\frac{1}{2}$，+∞）且p＜q＜r，A（p，g（p）），B（q，g（q）），C（r，g（r）），求证：kAB＞kBC（其中kAB，kBC分别为直线AB与BC的斜率）．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    5．函数f（x）=ax|log2x|-1有两个不同的零点，则实数a的取值范围是（　　）
    A．（1，10）B．（1，+∞）C．（0，1）D．（10，+∞）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    4．已知函数f（x）=$\frac{1}{2}$x2-2x+a2lnx，（a＞0）
    （Ⅰ）若函数y=f（x）在x∈（$\frac{1}{2}$，1）上有最大值，求a的取值范围；
    （Ⅱ）若a≥$\sqrt{6}$，n∈N*，且n≥2
    求证：
    ①$\sum_{i=1}^{n}$f（xi）＞0；
    ②a2ln$\frac{1}{n！}$＜$\frac{n（n+1）（2n-11）}{12}$
    （提示：12+22+33+…+n2=$\frac{n（n+1）（2n+1）}{6}$．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    3．函数f（x）=lnx-$\frac{2}{x}$的零点所在的大致区间是（　　）
    A．（0，1）B．（1，2）C．（2，e）D．（3，4）

    查看答案和解析>>

    科目： 来源： 题型：解答题

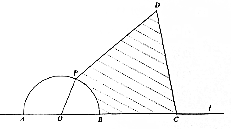    2．如图，直线l是湖岸线，O是l上一点，弧$\widehat{AB}$是以O为圆心的半圆形栈桥，C为湖岸线l上一观景亭，现规划在湖中建一小岛D，同时沿线段CD和DP（点P在半圆形栈桥上且不与点A，B重合）建栈桥，考虑到美观需要，设计方案为DP=DC，∠CDP=60°且圆弧栈桥BP在∠CDP的内部，已知BC=2OB=2（km），设湖岸BC与直线栈桥CD，DP是圆弧栈桥BP围成的区域（图中阴影部分）的面积为S（km2），∠BOP=θ
    （1）求S关于θ的函数关系式；
    （2）试判断S是否存在最大值，若存在，求出对应的cosθ的值，若不存在，说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

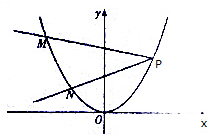    1．如图，点P（x0，$\frac{p}{2}$）（x0＞0）在抛物线x2=2py（p＞0）上．过P的直线PM，PN分别与抛物线交于点M（x1，y1）和N（x2，y2）．
    （Ⅰ）求x0的值；
    （Ⅱ）若PM，PN的斜率存在且倾斜角互补，试求直线MN的斜率．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    19．在△ABC中，tanA+tanB-$\sqrt{3}$tanAtanB=-$\sqrt{3}$，且a，b恰好为一元二次方程x2-mx+8=0的两根，则S△ABC=2$\sqrt{3}$．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    18．函数y=$\frac{\sqrt{3x+2}}{{x}^{2}-1}$的定义域为{x|x$≥-\frac{2}{3}$且x≠1}．

    查看答案和解析>>

    同步练习册答案