练习册

  • 练习册
  • 试题
    相关习题
     0  231850  231858  231864  231868  231874  231876  231880  231886  231888  231894  231900  231904  231906  231910  231916  231918  231924  231928  231930  231934  231936  231940  231942  231944  231945  231946  231948  231949  231950  231952  231954  231958  231960  231964  231966  231970  231976  231978  231984  231988  231990  231994  232000  232006  232008  232014  232018  232020  232026  232030  232036  232044  266669 

    科目： 来源： 题型：解答题

    8．已知p：$\frac{1}{x-2}$＜1，q：|x-a|＜1，若￢p是￢q的充分不必要条件，求实数a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    7．某卖场同时销售变频冷暖空调机和智能洗衣机，这两种产品的市场需求量大，有多少卖多少．今年五一假期该卖场要根据实际情况确定产品的进货数量，以达到总利润最大．已知两种产品直接受资金和劳动力的限制．根据过去销售情况，得到两种产品的有关数据如表：（表中单位：百元）试问：怎样确定两种货物的进货量，才能使五一期间的总利润最大，最大利润是多少？
    资金单位产品所需资金资金供应量
    空调机洗衣机
    成本3020440
    劳动力：工资710156
    单位利润108 

    查看答案和解析>>

    科目： 来源： 题型：解答题

    6．已知函数f（x）=sin（2ωx-$\frac{π}{6}}$）-4sin2ωx+2（{ω＞0}），其图象与x轴相邻的两个交点的距离为$\frac{π}{2}$．
    （I）求函数的f（x）解析式；
    （Ⅱ）若将f（x）的图象向左平移m（m＞0）个长度单位得到函数g（x）的图象恰好经过点（${-\frac{π}{3}$，0），求当m取得最小值时，g（x）在[${-\frac{π}{6}$，$\frac{7π}{12}}$]上的单调区间．

    查看答案和解析>>

    科目： 来源： 题型：填空题

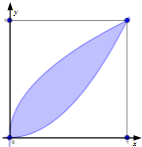
    5．如图，向边长为1的正方形内随机的投点，所投的点落在由y=x2和y=x${\;}^{\frac{1}{2}}}$围成的封闭图形的概率为$\frac{1}{3}$．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    4．已知函数f（x）=2ex+$\frac{1}{2}$ax2+ax+1有两个极值，则实数a的取值范围为（　　）
    A．（-∞，-2]B．（-∞，-2）C．（-2，+∞）D．（-∞，2）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    3．已知函数f（x）=mx-$\frac{m-1+2e}{x}$-lnx，m∈R，e为自然对数的底数，函数g（x）=$\frac{1}{xcosθ}$+lnx在区间[1，+∞）内为增函数，且θ∈（-$\frac{π}{2}$，$\frac{π}{2}$）．
    （1）当m=0时，求函数f（x）的单调区间和极值；
    （2）若当x∈[1，e]时，至少存在一个x0，使得f（x0）＞g（x0）成立，求实数m的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

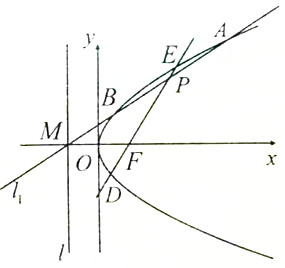    2．已知抛物线C：y2=2px（p＞0）的焦点F与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点重合，抛物线C的准线l与x轴的交点为M，过点M且斜率为k的直线l1交抛物线C于A，B两点，线段AB的中点为P，直线PF与抛物线C交于D，E两点
    （Ⅰ）求抛物线C的方程；
    （Ⅱ）若λ=$\frac{|MA|•|MB|}{|FD|•|FE|}$，写出λ关于k的函数解析式，并求实数λ的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

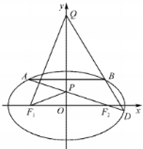    1．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{2}}{2}$，且椭圆上一点M与椭圆左右两个焦点构成的三角形周长为4+2$\sqrt{2}$．
    （1）求椭圆C的方程；
    （2）如图，设点D为椭圆上任意一点，直线y=m和椭圆C交于A、B两点，且直线DA、DB与y轴分别交于P、Q两点，试探究∠PF1F2和∠QF1F2之间的等量关系并加以证明．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    20．设平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$都是单位向量，且向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为60°，若$\overrightarrow{c}$=2x$\overrightarrow{a}$+y$\overrightarrow{b}$，其中x，y为正实数，则xy的最大值为（　　）
    A．$\frac{1}{6}$B．$\frac{1}{5}$C．$\frac{1}{4}$D．$\frac{1}{3}$

    查看答案和解析>>

    科目： 来源： 题型：填空题

    19．如图，在?ABCD中，点E为边AB的中点，BD与CE交于点P，若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$（x，y∈R），则2x+y=$\frac{5}{3}$；若点Q是△BCP内部（包括边界）一动点，且$\overrightarrow{AQ}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$（m，n∈R），则m+2n的取值范围为[1，3]．

    查看答案和解析>>

    同步练习册答案