练习册

  • 练习册
  • 试题
    相关习题
     0  232069  232077  232083  232087  232093  232095  232099  232105  232107  232113  232119  232123  232125  232129  232135  232137  232143  232147  232149  232153  232155  232159  232161  232163  232164  232165  232167  232168  232169  232171  232173  232177  232179  232183  232185  232189  232195  232197  232203  232207  232209  232213  232219  232225  232227  232233  232237  232239  232245  232249  232255  232263  266669 

    科目： 来源： 题型：选择题

    17．在极坐标系中，直线l的方程为ρsin（θ+$\frac{π}{4}$）=$\frac{\sqrt{2}}{2}$，则点A（2，-$\frac{π}{4}$）到直线l的距离为（　　）
    A．$\sqrt{2}$B．$\frac{\sqrt{2}}{2}$C．2-$\frac{\sqrt{2}}{2}$D．2+$\frac{\sqrt{2}}{2}$

    查看答案和解析>>

    科目： 来源： 题型：填空题

    16．（1）对于函数f（x），若在定义域内存在实数x满足f（-x）=-f（x）则称f（x）为局部函数，已知二次函数f（x）=ax2+2x-4a（a∈R，a≠0）是定义域在R上的局部函数，则满足f（-x）=-f（x）的x值是±2
    （2）若直角坐标平面内两点A、B满足条件：点A、B都在f（x）的图象上；点A、B关于原点对称，则对称点（A、B）对是函数的一个姊妹点对点对（A、B）与（B、A）可看做一个姊妹点对．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+2x，x＜0}\\{\frac{2}{{e}^{x}}，x≥0}\end{array}\right.$则f（x）的姊妹点对个数为2．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    15．函数f（x）=log3（1+x）-log3（1-x）的定义域是（-1，1），f（$\frac{1}{2}$）=1．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    14．2011年12月，吴某的工资纳税额是245元，若不考虑其它因素，则吴某该月工资收入为（　　）
    级数全月应纳税所得额税率（%）
    1不超过1500元3
    21500元-4500元10
    注：本表所称全月应纳税所得额是以每月收入额减去3500元（起征点）后的余额．
    A．7000元B．7500元C．6600元D．5950元

    查看答案和解析>>

    科目： 来源： 题型：解答题

    13．已知函数f（x）=lnx+$\frac{1}{x}$．
    （Ⅰ）求证：f（x）≥1；
    （Ⅱ）若x-1＞alnx对任意x＞1恒成立，求实数a的最大值．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    12．在如图所示的程序框图中，若输出i的值是3，则输入x的取值范围是（4，10]

    查看答案和解析>>

    科目： 来源： 题型：填空题

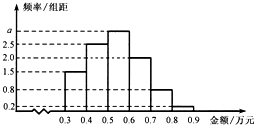    11．某电子商务公司对10000名网络购物者2014年度的消费情况进行统计，发现消费金额（单位：万元）都在区间[0.3，0.9]内，其频率分布直方图如图所示．直方图中的a=3．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    10．已知a=-2${∫}_{0}^{\frac{π}{2}}$（sin2$\frac{x}{2}$-$\frac{1}{2}$）dx，则二项式（ax+$\frac{1}{2ax}$）9的展开式中x的一次项系数为（　　）
    A．-$\frac{63}{16}$B．$\frac{63}{16}$C．-$\frac{63}{8}$D．$\frac{63}{8}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    9．抛掷一枚质地均匀的硬币，出现正面向上和反面向上的概率都为$\frac{1}{2}$，构造数列{an}，使an=$\left\{\begin{array}{l}{1，第n次正面向上}\\{-1，第n次把反面向上}\end{array}\right.$，记Sn=a1+a2+…+an，则S2≠0且S8=2的概率为（　　）
    A．$\frac{43}{128}$B．$\frac{43}{64}$C．$\frac{13}{128}$D．$\frac{13}{64}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    8．设函数f（x）=ax2+bx+c（a，b，c∈R且a＞0），则“f（f（-$\frac{b}{2a}$））＜0”是“f（x）与f（f（x））都恰有两个零点”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案