19．设函数f（x）=lnx-$\frac{1}{2}$ax²-bx．
（1）当a=3，b=2时，求函数f（x）的单调区间；
（2）令F（x）=f（x）+$\frac{1}{2}$ax²+bx+$\frac{a}{x}$（0＜x≤3），其图象上任意一点P（x₀，y₀）处切线的斜率k≤$\frac{1}{8}$恒成立，求实数a的取值范围；
（3）当a=b=0时，令H（x）=f（x）-$\frac{1}{x}$，G（x）=mx，若H（x）与G（x）的图象有两个交点A（x₁，y₁），B（x₂，y₂），求证：x₁x₂＞2e²．

18．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点为A₁，右焦点为F₂，过点F₂作垂直于x轴的直线交该椭圆于M，N两点，直线A₁M的斜率为$\frac{1}{2}$．
（1）求椭圆的离心率；
（2）若△A₁MN的外接圆在M处的切线与椭圆交于另一点D，且△F₂ MD的面积为$\frac{12}{7}$，求该椭圆方程．

17．某高中学校共有学生1800名，各年级男女学生人数如表．已知在全校学生中随机抽取1名，抽到高二女生的概率是0.16．

	高一年级	高二年级	高三年级
女生	324	x	280
男生	316	312	y

现用分层抽样的方法，在全校抽取45名学生，则应在高三抽取的学生人数为14．

16．已知集合A={x|x²-x≤0}，B={x|f（x）=lg（1-|x|）}，则A∪B=（-1，1]．

15．已知函数f（x）=|mx|-|x-1|（m＞0），若关于x的不等式f（x）≥0的解集中的整数恰有3个，则实数m的取值范围为（　　）

A．

（0，1]

B．

[$\frac{2}{3}$，$\frac{3}{4}$）

C．

[$\frac{4}{3}$，$\frac{3}{2}$）

D．

[$\frac{2}{3}$，2）

14．已知$\overrightarrow a$，$\overrightarrow b$，$\overrightarrow c$是同一平面内的三个向量，其中$\overrightarrow a$=（-1，2）．
（1）若|${\overrightarrow c}$|=$\sqrt{5}$，且$\overrightarrow a$∥$\overrightarrow c$，求$\overrightarrow c$的坐标；
（2）若|${\overrightarrow b}$|=$\frac{{\sqrt{5}}}{2}$，且（$\overrightarrow a$+$\overrightarrow{2b}$）⊥（2$\overrightarrow a$-$\overrightarrow b$），求|2$\overrightarrow a$+$\overrightarrow b}$|．

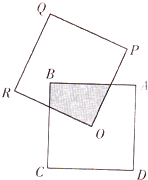13．小明爱好玩飞镖，现有图形构成如图所示的两个边长为2的正方形ABCD和OPQR，如果O点正好是正方形ABCD的中心，而正方形OPQR可以绕点O旋转，则小明射中阴影部分的概率是$\frac{1}{7}$．

12．已知极坐标的极点与平面直角坐标系的原点重合，极轴与x轴的正半轴重合，且长度单位相同．曲线C的极坐标方程为ρ=2（cosθ+sinθ）．
（Ⅰ）求曲线C的直角坐标方程；
（Ⅱ）直线l：$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$（t为参数）与曲线C交于A，B两点，与y轴交于点E，求$\frac{1}{|EA|}$+$\frac{1}{|EB|}$的值．

11．已知复数z满足：zi=2+i（i是虚数单位），则z对应的点在复平面的（　　）

A．

第一象限

B．

第二象限

C．

第三象限

D．

第四象限

10．若sinθ+cosθ=$\frac{{2\sqrt{2}-1}}{3}$（0＜θ＜π），则tanθ=-2$\sqrt{2}$．