练习册

  • 练习册
  • 试题
    相关习题
     0  232144  232152  232158  232162  232168  232170  232174  232180  232182  232188  232194  232198  232200  232204  232210  232212  232218  232222  232224  232228  232230  232234  232236  232238  232239  232240  232242  232243  232244  232246  232248  232252  232254  232258  232260  232264  232270  232272  232278  232282  232284  232288  232294  232300  232302  232308  232312  232314  232320  232324  232330  232338  266669 

    科目： 来源： 题型：解答题

    5．（1）等差数列{an}的前n项和是Sn，已知am-1+am+1-am2=0，S2m-1=38，求m；
    （2）设等差数列{an}的前n项和是Sn，若S3=9，S6=36，求a7+a8+a9；
    （3）若一个等差数列前3项的和为34，最后3项的和为146，且所有项的和为390，求这个数列的项数；
    （4）已知数列{an}的通项公式是an=4n-25，求数列{|an|}的前n项和并说出判断数列是等差数列的基本方法．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    4．已知函数f（x）=ax2-（a+2）x+lnx，其中a＞0，
    （1）若x=1是f（x）的极值点，求a；
    （2）若f（x）在区间[1，e]上的最小值为-2，求a的取值范围；
    （3）设g（x）=-$\int_0^x$[f（t）-lnt+at]dt，若对于任意的x1∈（2，+∞），都存在x2∈（1，+∞），使得g（x1）•g（x2）=1，求a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

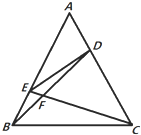    3．如图，在正△ABC中，点D、E分别在边AC、AB上，且$AD=\frac{1}{3}AC$，$AE=\frac{2}{3}AB$，BD、CE相交于点F．
    （Ⅰ）求证：A、E、F、D四点共圆，并求∠BFC的大小；
    （Ⅱ）求证：2BF•BD=CF•CE．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    2．已知函数f（x）=Asin（ωx+φ）（ A≠0，ω＞0，$-\frac{π}{2}＜φ＜\frac{π}{2}$）在$x=\frac{2π}{3}$时取得最大值，且它的最小正周期为π，则（　　）
    A．f（x）的图象过点（0，$\frac{1}{2}$）B．f（x）在$[{\frac{π}{6}，\frac{2π}{3}}]$上是减函数
    C．f（x）的一个对称中心是$（{\frac{5π}{12}，0}）$D．f（x）的图象的一条对称轴是x=$\frac{5π}{12}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    1．读如图的程序，若输入x=-2，则输出y=（　　）
    A．4B．0C．-2D．-4

    查看答案和解析>>

    科目： 来源： 题型：选择题

    20．已知实数x、y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$，则目标函数z=$\frac{y+2}{x}$的取值范围是（　　）
    A．[-$\frac{1}{3}$，+∞）B．[-1，$\frac{1}{2}$]C．（-∞，-1]∪[$\frac{1}{2}$，+∞）D．[-$\frac{1}{3}$，-1]

    查看答案和解析>>

    科目： 来源： 题型：解答题

    19．已知函数$f（x）=lnx+\frac{a}{2}{x^2}-（a+1）x$．
    （1）若曲线y=f（x）在x=1处的切线方程为y=-2，求f（x）的单调区间；
    （2）若x＞0时，$\frac{f（x）}{x}＜\frac{f'（x）}{2}$恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    18．下列命题正确的是（　　）
    A．在△ABC中，角A，B，C的对边分别是a，b，c，则a＞b是cosA＜cosB的充要条件
    B．已知$p：\frac{1}{x+1}＞0$，则$?p：\frac{1}{x+1}≤0$
    C．命题p：对任意的x∈R，x2+x+1＞0，则?p：对任意的x∈R，x2+x+1≤0
    D．存在实数x∈R，使$sinx+cosx=\frac{π}{2}$成立

    查看答案和解析>>

    科目： 来源： 题型：解答题

    17．已知函数f（x）=ex[x2-（m+2）x+2m+1]．
    （1）若函数f（x）在（0，2）上无极值，求实数m的值；
    （2）若m＞1，且存在实数x0∈（0，2），使得f（x0）是f（x）在[0，2]上的最大值，求实数m的取值范围；
    （3）若不等式$\frac{f（x）}{e^x}≥2lnx-\frac{1}{x^2}+2m+1$对于任意0＜x≤1恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．已知数列{an}满足：${a_1}∈{N^*}$，且${a_{n+1}}=\left\{\begin{array}{l}2{a_n}，{a_n}≤p\\ 2{a_n}-6，{a_n}＞p\end{array}\right.（{n=1，2，…}）$．记集合$M=\left\{{{a_n}\left|{n∈{N^*}}\right.}\right\}$．
    （1）若p=90，a2=6，写出数列{an}的前7项；
    （2）若p=18，集合M存在一个元素是3的倍数，证明：M的所有元素都是3的倍数．

    查看答案和解析>>

    同步练习册答案