18．已知圆C的圆心为y=$\frac{1}{4}$x2的焦点.且与直线4x+3y+2=0相切.则圆C的方程为( )A．${(x-1)^2}+{y^2}=\frac{36}{25}$B．${x^2}+——青夏教育精英家教网—

相关习题

0 232391 232399 232405 232409 232415 232417 232421 232427 232429 232435 232441 232445 232447 232451 232457 232459 232465 232469 232471 232475 232477 232481 232483 232485 232486 232487 232489 232490 232491 232493 232495 232499 232501 232505 232507 232511 232517 232519 232525 232529 232531 232535 232541 232547 232549 232555 232559 232561 232567 232571 232577 232585 266669

科目： 来源： 题型：选择题

18．已知圆C的圆心为y=$\frac{1}{4}$x²的焦点，且与直线4x+3y+2=0相切，则圆C的方程为（　　）

A．

${（x-1）^2}+{y^2}=\frac{36}{25}$

B．

${x^2}+{（y-1）^2}=\frac{36}{25}$

C．

（x-1）²+y²=1

D．

x²+（y-1）²=1

查看答案和解析>>

科目： 来源： 题型：选择题

17．已知l为平面α内的一条直线，α，β表示两个不同的平面，则“α⊥β”是“l⊥β”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

查看答案和解析>>

科目： 来源： 题型：选择题

16．已知一等差数列的前三项和为94，后三项和为116，各项和为280，则此数列的项数n为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目： 来源： 题型：解答题

15．

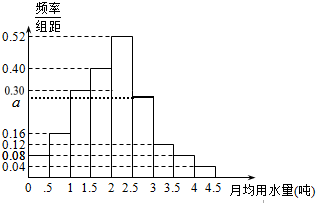我国是世界上严重缺水的国家，城市缺水尤为突出．某市为了制定合理的节水方案，从该市随机调查了100位居民，获得了他们某月的用水量，整理得到如图的频率分布直方图．
（Ⅰ）求图中a的值；
（Ⅱ）设该市有500万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由：
（Ⅲ）估计本市居民的月用水量平均数（同一组中的数据用该区间的中点值代表）．

查看答案和解析>>

科目： 来源： 题型：填空题

14．如图是一个几何体的三视图，若它的体积是$\frac{2}{3}$，则a=1．

查看答案和解析>>

科目： 来源： 题型：选择题

13．

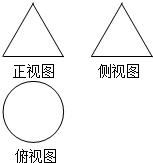如图所示，一个空间几何体的正视图和侧视图都是边长为4的等边三角形，俯视图是一个圆，那么其体积为（　　）

A．

$\frac{{4\sqrt{3}}}{3}π$

B．

$\frac{{8\sqrt{3}}}{3}π$

C．

$\frac{{\sqrt{3}}}{2}π$

D．

3π

查看答案和解析>>

科目： 来源： 题型：解答题

12．

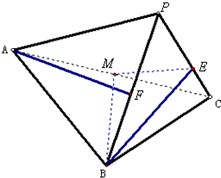在三棱锥P-ABC中，F，M分别是棱PB，AC的中点，E为PC上一动点．
（1）若AF∥平面MEB，试确定点E的位置，并证明你的结论．
（2）在满足（1）的条件下，求三棱锥C-MEB与三棱锥C-PAB的体积比．

查看答案和解析>>

科目： 来源： 题型：解答题

11．求值与化简
（1）（2$\frac{7}{9}$）^0.5+0.1^-2+（2$\frac{10}{27}$）${\;}^{-\frac{2}{3}}$-3π⁰+$\frac{37}{48}$；
（2）$\frac{1}{2}$lg$\frac{32}{49}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{245}$．

查看答案和解析>>

科目： 来源： 题型：解答题

10．已知等差数列{a_n}满足：a₅=3，前3项和S₃为$\frac{9}{2}$．
（1）求数列{a_n}的通项公式；
（2）求数列{$\frac{1}{{{a_n}{a_{n+2}}}}$}的前n项和．

查看答案和解析>>

科目： 来源： 题型：选择题

9．