10．已知一个动点M在圆x²+y²=36上移动，它与定点Q（4，0）所连线段的中点为P，则点P的轨迹方程（x-2）²+y²=9．

9．（文）已知椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1（a＞b＞0），F₁，F₂是它的左右焦点，过F₁的直线AB与椭圆交于AB两点，则△ABF₂的周长为（　　）

A．

8

B．

10

C．

32

D．

16

8．已知定义在R上的奇函数f（x），当x＞0时，f（x）=lnx-ax+1（a∈R）．
（1）求动点f（x）的解析式；
（2）当a=1，求函数f（x）的单调区间；
（3）若函数y=f（x）在R上恰好有5个零点，求实数a的取值范围．

7．如图，设椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右焦点为F₁，F₂，上顶点为A，点B和点F₂关于F₁对称，且AB⊥AF₂，A，B，F₂三点确定的圆M恰好与直线$x-\sqrt{3}y-3=0$相切．
（1）求椭圆的方程C；
（2）过F₁作一条与两坐标轴都不垂直的直线l交椭圆于P，Q零点，在x轴上是否存在点N，使得NF₁恰为△PNQ的内角平分线，若存在，求出点N的坐标，若不存在，请说明理由．

6．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，点O是对角线AC与BD的交点，M是PD上的点，且AB=2，∠BAD=60°．
（1）求证：平面PBD⊥平面PAC；
（2）当OM∥平面PAB且三棱锥M-BCD的体积等于$\frac{{\sqrt{3}}}{4}$时，求点C到面PBD的距离．

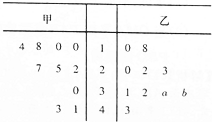5．某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量（单位：台），并根据这10个卖场的销售情况，得到如图所示的茎叶图，为了鼓励卖场，在同型号汽车的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”
（1）求在这10个卖场中，甲型号汽车的“星级卖场”的个数；
（2）若在这10个卖场中，乙型号汽车销售量的平均数为26.7，求a＜b的概率；
（3）若a=1，记乙型号汽车销售量的方差为s²，根据茎叶图推断b为何值时，s²达到最小值（只写出结论）
注：方差${s^2}=\frac{1}{n}[（{x_1}-\overline x）+（{x_2}-\overline x）+…+（{x_n}-\overline x）]$其中$\overline x$为x₁，x₂，…，x_n的平均数．

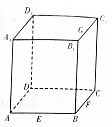4．已知点E、F、G分别为正方体ABCD-A₁B₁C₁D₁的棱AB、BC、$B_1^{\;}{C_1}$的中点，如图，则下列命题为假命题的是（　　）

	A．	点P在直线FG上一定，总有AP⊥DE
	B．	点Q在直线BC1上运动时，三棱锥A-D1QC的体积为定值
	C．	点M是正方体面A1B1C1D1内的点到点D和点C1距离相等的点，则M的轨迹是一条直线
	D．	过F，D1，G的截面是正方形

3．已知集合U=R，A={x|0≤x≤2}，B={y|y=2^x，x∈R}，则（∁_UA）∩B=（　　）

A．

（-∞，0）

B．

（0，1）

C．

（1，2]

D．

（2，+∞）

2．抛物线y=$\frac{1}{8}{x^2}$的准线方程是（　　）

A．

x=-2

B．

x=-4

C．

y=-2

D．

y=-4

1．双曲线x²-y²=8的在左、右焦点分别是F₁、F₂，点P_n（x_n，y_n）（n=1，2，3，…）在其右支上，且满足|P_n+1F₂|=|P_nF₁|，P₁F₂⊥F₁F₂，则x₂₀₁₆的值是8064．