科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

3．设函数f（x）是定义在区间（-∞，+∞）上以2为周期的函数，记I_k=（2k-1，2k+1]（k∈Z）．已知当x∈I₀时，f（x）=x²，如图．
（1）求函数f（x）的解析式；
（2）求使方程f（x）=ax在I_k（k∈N^*）上有两个不相等实数根的关于a的集合M_k．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

1．某校有1400名考生参加市模拟考试，现采用分层抽样的方法从文、理考生中分别抽取20份和50份数学试卷，进行成绩分析．得到下面的成绩频率分布表：

分数分值	[0，30）	[30，60）	[60，90）	[90，120）	[120，150）
文科频数	2	4	8	3	3
理科频数	3	7	12	20	8

（1）估计文科数学平均分及理科考生的及格人数（90分为及格分数线）；
（2）在试卷分析中，发现概念性失分非常严重，统计结果如下：

	文科	理科
概念	15	30
其它	5	20

问是否有90%的把握认为概念失分与文、理考生的不同有关？（本题可以参考独立性检验临界值表）
附参考公式与数据：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$

P（K2≥k）	0.5	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

科目： 来源： 题型：解答题

科目： 来源： 题型：填空题

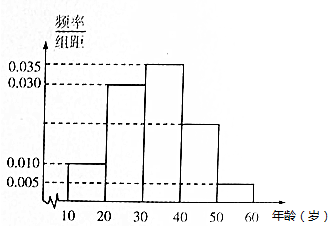19．为了调查市民对某活动的认可程度，研究人员对其所在地区年龄在10～60岁间的n位市民作出调查，并将统计结果绘制成频率分布直方图如图所示，若被调查的年龄在20～30岁间的市民有480人，则可估计被调查的年龄在40～50岁间的市民有320人．

科目： 来源： 题型：填空题

科目： 来源： 题型：解答题

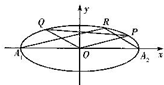17．如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右顶点分别为A₁，A₂，P，Q，T为椭圆异于A₁，A₂的点，若椭圆C的焦距为2$\sqrt{2}$，且椭圆过点M（$\frac{\sqrt{2}}{2}$，-$\frac{\sqrt{7}}{2}$）．
（1）求椭圆C的方程；
（2）若△OPQ的面积为$\sqrt{2}$，A₁R∥OP，求证：OQ∥A₂R．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题