练习册

  • 练习册
  • 试题
    相关习题
     0  233558  233566  233572  233576  233582  233584  233588  233594  233596  233602  233608  233612  233614  233618  233624  233626  233632  233636  233638  233642  233644  233648  233650  233652  233653  233654  233656  233657  233658  233660  233662  233666  233668  233672  233674  233678  233684  233686  233692  233696  233698  233702  233708  233714  233716  233722  233726  233728  233734  233738  233744  233752  266669 

    科目： 来源： 题型：选择题

    4．已知f（x）在（-∞，0]上是单调递增的，且图象关于y轴对称，若f（x-2）＞f（2），则x的取值范围是（　　）
    A．（-∞，0）∪（4，+∞）B．（-∞，2）∪（4，+∞）C．（2，4）D．（0，4）

    查看答案和解析>>

    科目： 来源： 题型：选择题

    3．下列函数中，是偶函数，且在区间（0，1）上为增函数的是（　　）
    A．y=|x|B．y=3-xC．y=$\frac{1}{x}$D．y=-x2+4

    查看答案和解析>>

    科目： 来源： 题型：选择题

    2．已知a＞0且a≠1，下列四组函数中表示相等函数的是（　　）
    A．$y={log_a}{x^2}$与y=2logaxB．y=2x与$y={log_a}{a^{2x}}$
    C．$y=\sqrt{{x^2}-4}$与$y=\sqrt{x+2}•\sqrt{x-2}$D．$y=\sqrt{x^2}$与y=x

    查看答案和解析>>

    科目： 来源： 题型：选择题

    1．集合A={y|y=$\sqrt{x-1}$}，B={x|log2（x-2）≤1}，则A∩B（　　）
    A．[1，4]B．[0，4]C．[0，2]D．（2，4]

    查看答案和解析>>

    科目： 来源： 题型：选择题

    20．设f（x）=$\left\{\begin{array}{l}{x^2}-1，x＜2\\ 3x，x≥2\end{array}$，则f（f（-2））的值为（　　）
    A．3B．6C．9D．12

    查看答案和解析>>

    科目： 来源： 题型：解答题

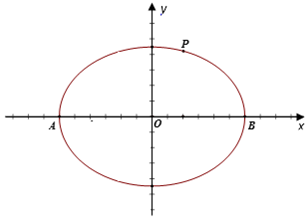    19．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{2}{3}$，b=$\sqrt{5}$．
    （1）求椭圆C的标准方程；
    （2）F1，F2分别为椭圆的左、右焦点，A、B为椭圆的左、右顶点，P为椭圆C上的点，求证：以PF2为直径的圆与以AB为直径的圆相切；
    （3）过左焦点F1作互相垂直的弦MN与GH，判断MN的中点与GH的中点所在直线l是否过x轴上的定点，如果是，求出定点坐标，如果不是，说出理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．已知双曲线C的焦点与椭圆$\frac{{x}^{2}}{35}$+$\frac{{y}^{2}}{10}$=1的焦点相同，且渐近线方程为y=±$\frac{4}{3}$x．
    （1）求双曲线C的标准方程；
    （2）设F1为双曲线的左焦点，P为双曲线C的右支上一点，且线段PF1的中点在y轴上，求△PF1F2的面积．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    17．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与直线x+y-1=0相交于A、B两点，若a∈[$\sqrt{2}$，$\sqrt{5}$]，且以AB为直径的圆经过坐标原点O，则椭圆离心率e的取值范围为[$\frac{\sqrt{6}}{3}$，$\frac{2\sqrt{2}}{3}$]．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    16．若关于x的不等式4x+x-a≤$\frac{3}{2}$在x∈[0，$\frac{1}{2}$]上恒成立，则实数a的取值范围是（　　）
    A．（-∞，-$\frac{1}{2}$]B．（0，1]C．[-$\frac{1}{2}$，1]D．[1，+∞）

    查看答案和解析>>

    科目： 来源： 题型：选择题

    15．{an}满足an+an+1=$\frac{1}{2}$（n∈N且n≥1），a2=1，则S21 为（　　）
    A．$\frac{9}{2}$B．$\frac{11}{2}$C．6D．5

    查看答案和解析>>

    同步练习册答案