练习册

  • 练习册
  • 试题
    相关习题
     0  233653  233661  233667  233671  233677  233679  233683  233689  233691  233697  233703  233707  233709  233713  233719  233721  233727  233731  233733  233737  233739  233743  233745  233747  233748  233749  233751  233752  233753  233755  233757  233761  233763  233767  233769  233773  233779  233781  233787  233791  233793  233797  233803  233809  233811  233817  233821  233823  233829  233833  233839  233847  266669 

    科目： 来源： 题型：填空题

    18．log225+${log_{\frac{1}{2}}}$8+log416+${log_{\sqrt{2}}}\frac{1}{5}$=-1．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    17．已知m∈R，函数f（x）=$\left\{\begin{array}{l}{|2x+1|，x＜1}\\{lo{g}_{2}（x-1），x＞1}\end{array}$，g（x）=x2-2x+2m-1，下列叙述中正确的有②
    ①函数y=f（f（x））有4个零点；
    ②若函数y=g（x）在（0，3）内有零点，则-1＜m≤1；
    ③函数y=f（x）+g（x）有两个零点的充要条件是m≤-$\frac{1}{2}$或m≥-$\frac{1}{8}$；
    ④若函数y=f（g（x））-m有6个零点则实数m的取值范围是（0，$\frac{3}{5}$）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．已知数列{an}各项都为正数，且a1=e，lnan+1-lnan=1（n∈N*）
    （1）求数列{lnan}的通项公式；
    （2）令bn=$\frac{1}{ln{a}_{n+1}•ln{a}_{n}}$，求数列{bn}的前n项和Sn．

    查看答案和解析>>

    科目： 来源： 题型：解答题

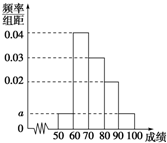    15．某班100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
    （1）根据频率分布直方图，估计这100名学生语文成绩的平均数、中位数、众数；
    （2）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求数学成绩在[50，80）之外的人数．
    分数段[50，60）[60，70）[70，80）[80，90）
    x：y1：12：13：44：5

    查看答案和解析>>

    科目： 来源： 题型：解答题

    14．已知等差数列{an}（n∈N*）的前n项和为Sn，且a3=5，S3=9
    （1）求数列{an}的通项公式；
    （2）若${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$，求数列{bn}的前n项和Tn；
    （3）若等比数列{cn}（n∈N*）中，c2=a2，c3=a5，求数列{cn}的前n项和Qn．

    查看答案和解析>>

    科目： 来源： 题型：选择题

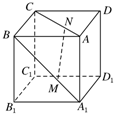    13．如图所示，正方体ABCD-A1B1C1D1的棱长为a，M，N分别为A1B和AC上的点，A1M=AN=$\frac{\sqrt{2}a}{3}$，则MN与平面BB1C1C的位置关系是（　　）
    A．相交B．平行C．垂直D．不能确定

    查看答案和解析>>

    科目： 来源： 题型：选择题

    12．${（a\root{3}{x}-\frac{1}{{\sqrt{x}}}）^5}$展开式中各项系数的和为32，则该展开式中的常数项为（　　）
    A．-540B．-270C．540D．270

    查看答案和解析>>

    科目： 来源： 题型：解答题

    11．二次函数f（x）满足f（x+1）-f（x）=2x且f（0）=1．
    （1）求f（x）的解析式；
    （2）当x∈[-1，1]时，不等式f（x）＞2x+m恒成立，求实数m的取值范围．
    （3）设函数f（x）在区间[a，a+1]上的最小值为g（a），求g（a）的表达式．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    10．设命题p：函数$y=sin（2x+\frac{π}{6}）$的图象关于直线$x=\frac{π}{6}$对称；命题q：函数y=|3x-1|在[-1，+∞）上是增函数．则下列判断错误的是（　　）
    A．p为假B．￢q为真C．p∧q为假D．p∨q为真

    查看答案和解析>>

    科目： 来源： 题型：解答题

    9．在直角坐标系xOy中，以原点为O极点，以x轴正半轴为极轴，圆C的极坐标方程为$ρ=4\sqrt{2}sin（\frac{3π}{4}-θ）$
    （1）将圆C的极坐标方程化为直角坐标方程；
    （2）过点P（0，2）作斜率为$\sqrt{3}$直线l与圆C交于A，B两点，试求$|{\frac{1}{|PA|}-\frac{1}{|PB|}}|$的值．

    查看答案和解析>>

    同步练习册答案