练习册

  • 练习册
  • 试题
    相关习题
     0  234231  234239  234245  234249  234255  234257  234261  234267  234269  234275  234281  234285  234287  234291  234297  234299  234305  234309  234311  234315  234317  234321  234323  234325  234326  234327  234329  234330  234331  234333  234335  234339  234341  234345  234347  234351  234357  234359  234365  234369  234371  234375  234381  234387  234389  234395  234399  234401  234407  234411  234417  234425  266669 

    科目： 来源： 题型：选择题

    15．已知函数f（x）=2sinxcos|x|（x∈R），则下列叙述错误的是（　　）
    A．f（x）的最大值是1B．f（x）是奇函数
    C．f（x）在[0，1]上是增函数D．f（x）是以π为最小正周期的函数

    查看答案和解析>>

    科目： 来源： 题型：选择题

    14．在△ABC中，“$\overrightarrow{CA}•\overrightarrow{CB}＞0$”，是“△ABC为锐角三角形”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目： 来源： 题型：选择题

    13．6名志愿者选4人去“”鸟巢”和“水立方”实地培训，每处2人，其中乙不能去“水立方”，则选派方法有（　　）
    A．60B．70C．80D．90

    查看答案和解析>>

    科目： 来源： 题型：解答题

    12．已知抛物线C的顶点为坐标原点，焦点为F（1，0），直线l与抛物线C相交于A，B两点，且线段AB的中点为M（2，2）．
    （1）求抛物线的C的方程；
    （2）求直线l的方程．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    11．已知关于x的不等式|x-2|-|x-3|≤m对x∈R恒成立．
    （1）求实数m的最小值；
    （2）若a，b，c为正实数，k为实数m的最小值，且$\frac{1}{a}$+$\frac{1}{2b}$+$\frac{1}{3c}$=k，求证：a+2b+3c≥9．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    10．下列函数中，最小值为2的是（　　）
    A．y=$\frac{1}{x}$+x （x＜0）B．y=$\frac{1}{x}$+1 （x≥1）C．y=$\sqrt{x}$+$\frac{4}{\sqrt{x}}$-2  （x＞0）D．y=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$

    查看答案和解析>>

    科目： 来源： 题型：填空题

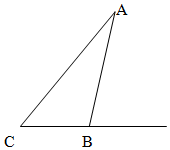    9．如图为了立一块广告牌，要制造一个三角形的支架   三角形支架形状如图，要求∠ACB=60°，BC的长度大于1米，且AC比AB长0.5米，为了广告牌稳固，要求AC的长度越短越好，则AC最短为2+$\sqrt{3}$米．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    8．在平面直角坐标系xOy中，圆O：x2+y2=1，P为直线l：x=$\frac{4}{3}$上一点．
    （1）若点P在第一象限，且OP=$\frac{5}{3}$，求过点P圆O的切线方程；
    （2）若存在过点P的直线交圆O于点A，B，且B恰为线段AP的中点，求点P纵坐标的取值范围；
    （3）设直线l动点Q，⊙Q与⊙O相外切，⊙Q交L于M、N两点，对于任意直径MN，平面上是否存在不在直线L上的定点A，使得∠MAN为定值？若存在，直接写出点A的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

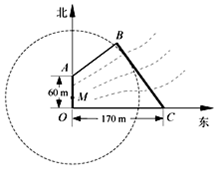    7．如图，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区．规划要求：新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上并与BC相切的圆．经测量，点A位于点O正北方向60m处，点C位于点O正东方向170m处（OC为河岸），tan∠BCO=$\frac{4}{3}$．
    （1）当点M与A重合时，求圆形保护区的面积；
    （2）若古桥两端O和A到该圆上任意一点的距离均不少于80m．当OM多长时，点M到直线BC的距离最小？

    查看答案和解析>>

    科目： 来源： 题型：解答题

    6．（1）过原点作直线l的垂线，若垂足为A（-2，3），求直线l的方程；
    （2）三角形三个顶点是A（4，0），B（6，7），C（0，3），求AB边上的高所在的直线方程．

    查看答案和解析>>

    同步练习册答案