7．已知a，b为常数，且a≠0，f（x）=ax²+bx，f（2）=0，方程f（x）=x有两个相等实数根．
（1）求函数f（x）的解析式；
（2）当x∈[1，2]时，求f（x）的值域；
（3）若F（x）=f（x）-f（-x）+$\frac{m}{{x}^{2}}$，试判断F（x）的奇偶性，并说明理由．

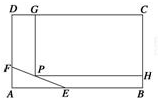6．如图所示，为了保护环境，实现城市绿化，某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC，建造住宅小区公园，但不能越过文物保护区三角形AEF的边线EF．已知AB=CD=200m，BC=AD=160m，AF=40m，AE=60m，问如何设计才能使公园占地面积最大，求出最大面积．

5．若定义在R上的偶函数f（x）对任意x₁，x₂∈[0，+∞）（x₁≠x₂），有$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}$＜0，则（　　）

A．

f（3）＜f（-2）＜f（1）

B．

f（1）＜f（-2）＜f（3）

C．

f（1）＜f（3）＜f（-2）

D．

f（-2）＜f（3）＜f（1）

4．下列各组对象：
（1）高中数学中所有难题；
（2）所有偶数；
（3）平面上到定点O距离等于5的点的全体；
（4）全体著名的数学家．
其中能构成集合的个数为（　　）

A．

1个

B．

2个

C．

3个

D．

4个

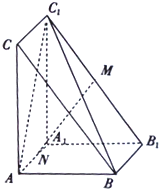3．如图，在三棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC，AB=AA₁=2，AC=$\sqrt{5}$，BC=3，M，N分别为B₁C₁、AA₁的中点．
（1）求证：平面ABC₁⊥平面AA₁C₁C；
（2）求证：MN∥平面ABC₁，并求M到平面ABC₁的距离．

2．若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“同族函数”，那么y=x²，值域为{1，9}的“同族函数”共有9个．

1．设函数f（x）=ax²+bx+3a+b的图象关于y轴对称，且其定义域为[a-1，2a]（a，b∈R），则函数f（x）的单调减区间为[$-\frac{2}{3}$，0]．

20．已知集合A={x|-2＜x＜3}，B={x|m＜x＜m+9}．
（1）若A∪B=B，求实数m的取值范围
（2）若A∩B≠∅，求实数m的取值范围．

19．已知函数f（x）=sin2x-$\frac{\sqrt{3}}{2}$（x∈[0，π]），g（x）=x+3，点P（x₁，y₁），Q（x₂，y₂）分别位于f（x），g（x）的图象上，则（x₁-x₂）²+（y₁-y₂）²的最小值为（　　）

A．

$\frac{（π+18）^{2}}{72}$

B．

$\frac{\sqrt{2}π}{12}$

C．

$\frac{（π+18）^{2}}{12}$

D．

$\frac{（π-3\sqrt{3}+15）^{2}}{72}$

18．某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：

日期	12月1日	12月2日	12月3日	12月4日	12月5日
温差x（℃）	10	11	13	12	8
发芽数y（颗）	23	25	30	26	16

该农科所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．
（1）求选取的2组数据恰好是不相邻2天数据的概率．
（2）若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求出y关于x的线性回归方程$\widehaty=bx+a$；假设由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？
附：参考公式：b=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\widehata=\overline y-\widehatb\overline x$．