12．已知定义在R上的奇函数f（x）满足f（$\frac{3}{2}$-x）=f（x），f（-2）=-3，数列{a_n}的前n项和为S_n，且a₁=-1，S_n=2a_n+n（n∈N^*），则f（a₅）+f（a₆）的值是（　　）

A．

1

B．

2

C．

3

D．

4

11．下列命题中的真命题有（　　）
①做9次抛掷一枚均匀硬币的试验，结果有5次出现正面，因此出现正面的概率是$\frac{5}{9}$；
②盒子中装有大小均匀的3个红球，3个黑球，2个白球，那么每种颜色的球被摸到的可能性相同；
③从-4，-3，-2，-1，0，1，2，3中任取一个数，取得的数小于0和不小于0的可能性相同；
④二进制数1101化为八进制数是15．

A．

1个

B．

2个

C．

3个

D．

4个

10．已知某运动员每次投篮命中的概率都为50%．现采用随机模拟的方法估计该运动员四次投篮恰有两次命中的概率：先由计算器算出0到9之间取整数值的随机数，指定0，1，2，3，4表示命中，5，6，7，8，9表示不命中；再以每四个随机数为一组，代表四次投篮的结果．经随机模拟产生了20组随机数：
9075   9660   1918   9257    2716    9325    8121    4589   5690    6832
4315   2573   3937   9279    5563    4882    7358    1135   1587    4989
据此估计，该运动员四次投篮恰有两次命中的概率为（　　）

A．

0.40

B．

0.35

C．

0.30

D．

0.25

9．两人轮流投掷骰子，每人每次投掷两颗，第一个使两颗骰子点数和大于6者为胜，否则由另一人投掷，先投掷人的获胜概率是$\frac{12}{17}$（写出计算过程）

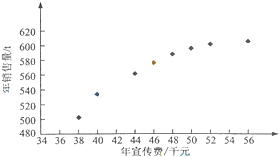8．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费x_i和年销售量y_i（i=1，2，…，8）数据作了初步处理，得到如图的散点图及一些统计量的值．

$\overline{x}$	$\overline{y}$	$\overline{w}$	$\sum_{i=1}^{8}$（xi-$\overline{x}$）2	$\sum_{i=1}^{8}$（wi-$\overline{w}$）2	$\sum_{i=1}^{8}$（xi-$\overline{x}$）（yi-$\overline{y}$）	$\sum_{i=1}^{8}$（wi-$\overline{w}$）（yi-$\overline{y}$）
46.6	563	6.8	289.8	1.6	1469	108.8

表中${w_i}=\sqrt{x_i}$，$\overrightarrow w$=$\frac{1}{8}$$\sum_{i=1}^8{w_i}$
（Ⅰ）根据散点图判断，y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
（Ⅲ）已知这种产品的年利率z与x、y的关系为z=0.2y-x．根据（Ⅱ）的结果回答下列问题：
（ⅰ）年宣传费x=49时，年销售量及年利润的预报值是多少？
（ⅱ）年宣传费x为何值时，年利率的预报值最大？
附：对于一组数据（u₁，v₁），（u₂，v₂），…，（u_n，v_n），其回归线v=α+βu的斜率和截距的最小二乘估计分别为：$\stackrel{∧}{β}$=$\frac{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）（{v}_{i}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）}$，$\stackrel{∧}{α}$=$\overline{v}$-$\stackrel{∧}{β}$$\overline{u}$．

7．（Ⅰ）用辗转相除法求567与405的最大公约数．
（Ⅱ）用更相减损术求2004与4509的最大公约数．

6．甲乙两人相约在上午9：00至10：00之间东方明珠前见面．可是两人都是大忙人，只能在那里停留5分钟就要匆匆离去，则两人见面的概率是$\frac{23}{144}$．

5．给出一个程序框如图，则输出x的值是（　　）

A．

45

B．

43

C．

41

D．

39

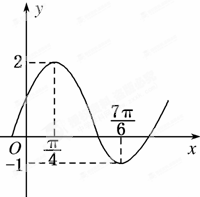4．将函数f（x）=Asin（ωx+φ）+k（A＞0，ω＞0，0＜φ＜π）的图象向右平移$\frac{2π}{3}$个单位，所得曲线的一部分如图所示，则f（x）的解析式为（　　）

	A．	f（x）=$\frac{3}{2}$sin（$\frac{12}{11}$x-$\frac{21π}{22}$）+1		B．	f（x）=$\frac{3}{2}$sin（$\frac{12}{11}$x+$\frac{21π}{22}$）+$\frac{1}{2}$
	C．	f（x）=2sin（$\frac{11}{12}$x+$\frac{21π}{22}$）-$\frac{1}{2}$		D．	f（x）=$\frac{3}{2}$sin（$\frac{12}{11}$x+$\frac{5π}{22}$）+$\frac{1}{2}$

3．已知10件产品中有3件次品，从中任取2件，取到次品的件数为随机变量，用X表示，那么X的取值为（　　）

A．

0，1

B．

0，2

C．

1，2

D．

0，1，2