9．已知函数f(x)=-3sin2x-4cosx+2.则该函数的最大值和最小值的差为( )A．6B．4C．$\frac{25}{3}$D．-$\frac{7}{3}$——青夏教育精英家教网—

相关习题

0 234542 234550 234556 234560 234566 234568 234572 234578 234580 234586 234592 234596 234598 234602 234608 234610 234616 234620 234622 234626 234628 234632 234634 234636 234637 234638 234640 234641 234642 234644 234646 234650 234652 234656 234658 234662 234668 234670 234676 234680 234682 234686 234692 234698 234700 234706 234710 234712 234718 234722 234728 234736 266669

科目： 来源： 题型：选择题

9．已知函数f（x）=-3sin²x-4cosx+2，则该函数的最大值和最小值的差为（　　）

A．

B．

C．

$\frac{25}{3}$

D．

-$\frac{7}{3}$

查看答案和解析>>

科目： 来源： 题型：选择题

8．点P在△ABC所在平面上，若$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{AB}$，且S_△ABC=12，则△PAB的面积为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目： 来源： 题型：解答题

7．已知函数f（x）=（sinx+cosx）²+2cos²x
（1）求f（x）的单调递减区间
（2）求f（x）在$x∈[0，\frac{π}{2}]$时的值域
（3）叙述由$y=\sqrt{2}sinx$到y=f（x）的图象的变换过程．

查看答案和解析>>

科目： 来源： 题型：解答题

6．

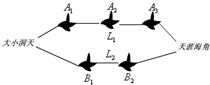（理）“十一黄金周”期间三亚景区迎来了游客高峰期．游客小李从“大小洞天”到景区“天涯海角”景区有L₁，L₂两条路线（如图），路线L₁上有A₁，A₂，A₃三个风景点，各风景点遇到堵塞的概率均为$\frac{2}{3}$；L₂路线上有B₁，B₂两个风景点，各风景点遇到堵塞的概率依次为$\frac{3}{4}$，$\frac{3}{5}$．
（1）若走L₁路线，求最多遇到1次堵塞的概率；
（2）按照“平均遇到堵塞次数最少”的要求，请你帮助小李从上述两条路线中选择一条最好的旅游路线，并说明理由．

查看答案和解析>>

科目： 来源： 题型：填空题

5．给出下列四个命题：
①线性相关系数r的绝对值越接近于1，表明两个随机变量线性相关性越强；
②已知X～B（n，p），E（X）=2，D（X）=1.6，则n，p的值分别为10，0.2；
③过抛物线y²=4x的焦点作直线交抛物线于A（x₁，y₁），B（x₂，y₂）两点，如果x₁+x₂=6，那
么|AB|等于8；
④己知直线l₁：ax+3y-l=0，l₂：x+by+l=0，则l₁⊥l₂的充要条件是b=-3．
其中真命题的是①②③．

查看答案和解析>>

科目： 来源： 题型：填空题

4．设点集M={（x，y）|xcosθ+ysinθ-sinθ-1=0（0≤θ≤2π）}，集合M在坐标平面xoy内形成区域的边界构成曲线C，曲线C的中心为T，圆N：（x-2-5cosθ）²+（y-5sinθ）²=1，过圆N上任一点P分别作曲线C的两切线PE，PF，切点分别为E，F，则$\overrightarrow{TE}•\overrightarrow{TF}$的范围为[-$\frac{\sqrt{5}+1}{4}$，$\frac{\sqrt{5}-1}{4}$]．

查看答案和解析>>

科目： 来源： 题型：解答题

3．已知集合E={x||x-1|≥m}，F=$\{x|\frac{10}{x+6}＞1\}$．
（1）若m=3，求E∩F；
（2）若E∩F=∅，求实数m的取值范围．

查看答案和解析>>

科目： 来源： 题型：选择题

2．函数y=（$\frac{1}{2}$）${\;}^{{x}^{2}}$^+4x的值域为（　　）

A．

[0，16]

B．

（0，16]

C．

（16，+∞）