
科目: 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | ?x≥0,ex<x+1 | B. | ?x≥0,ex>x+1 | C. | ?x≥0,ex≥x+1 | D. | ?x≥0,ex≥x+1 |
查看答案和解析>>
科目: 来源: 题型:解答题
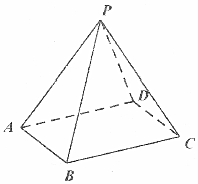 在底面是菱形的四棱锥P-ABCD中,∠BAD=60°,AB=2,PA=PC=2,PB=PD=$\sqrt{2}$.
在底面是菱形的四棱锥P-ABCD中,∠BAD=60°,AB=2,PA=PC=2,PB=PD=$\sqrt{2}$.查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:选择题
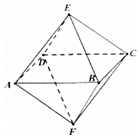
| A. | 不平行的两条棱所在的直线所成的角是60o或90o | |
| B. | 四边形AECF是正方形 | |
| C. | 点A到平面BCE的距离为$\frac{\sqrt{6}}{3}$ | |
| D. | 该八面体的顶点不会在同一个球面上. |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | 2π | C. | 4π | D. | π |
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为45°,AB和CD是底面圆O上的两条平行的弦,∠COD=60°.
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为45°,AB和CD是底面圆O上的两条平行的弦,∠COD=60°.查看答案和解析>>
科目: 来源: 题型:解答题
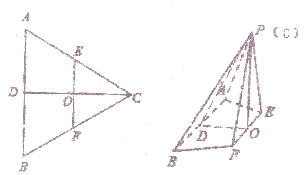 如图,在边长为4的等边三角形ABC中,点D,E,F分别是边AB,AC,BC的中点,DC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的四棱锥P-ABFE,且PB=$\sqrt{10}$.
如图,在边长为4的等边三角形ABC中,点D,E,F分别是边AB,AC,BC的中点,DC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的四棱锥P-ABFE,且PB=$\sqrt{10}$.查看答案和解析>>
科目: 来源: 题型:解答题
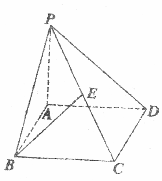 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com