9．已知线段AB上有9个确定的点（包括端点A与B）．现对这些点进行往返标数（从A→B→A→B→…进行标数，遇到同方向点不够数时就“调头”往回数）．如图：在点A上标1称为点1，然后从点1开始数到第二个数，标上2，称为点2，再从点2开始数到第三个数，标上3，称为点3（标上数n的点称为点n），…，这样一直继续下去，直到1，2，3，…，2013都被标记到点上．则点2013上的所有标记的数中，最小的是2．

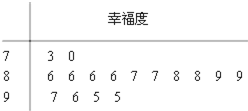8．某权威机构发布了2014年度“城市居民幸福排行榜”，某市成为本年度城市最“幸福城”．随后，该市某校学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度．现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：
（1）指出这组数据的众数和中位数；
（2）若幸福度不低于9.5分，则称该人的幸福度为“极幸福”．求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
（3）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记ξ表示抽到“极幸福”的人数，求ξ的分布列及数学期望．

7．同时掷六个面分别标有数字1、2、3、4、5、6的质地均匀和大小相同的两枚正方形骰子，计算向上的点数之和是5的概率是$\frac{1}{9}$．

6．已知$f（x）=sin[\frac{π}{3}（x+1）]-\sqrt{3}cos[\frac{π}{3}（x+1）]$，则f（1）+f（2）+f（3）+…+f（2013）=（　　）

A．

-$\sqrt{3}$

B．

$\sqrt{3}$

C．

-2$\sqrt{3}$

D．

2$\sqrt{3}$

5．有四个游戏盘，如图所示，（其中A的外形为正方形；B的外形为正六边形；C的外形为正方形；D．的外形为圆，D．的阴影部分为等腰直角三角形）撒一粒黄豆到游戏盘，如果落在阴影部分，则可中奖．你希望中奖机会大，你应当选择的游戏盘为（　　）

A．

B．

C．

D．

4．已知函数f（x）=x²+aln（x+1），其中a≠0
（1）若a=-4，求f（x）的极值；
（2）判断函数f（x）的单调性．

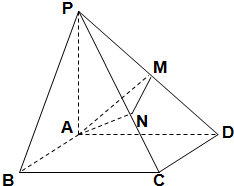3．四棱锥P-ABCD的底面是矩形，PA⊥平面ABCD，且PA=AD=2AB，点M，N分别在侧棱PD，PC上，且$\overrightarrow{PM}=\overrightarrow{MD}$．
（1）求证：平面AMN⊥平面PCD；
（2）若$\overrightarrow{PN}=2\overrightarrow{NC}$，求平面AMN与平面PAB所成锐角的二面角的余弦值．

2．在一次物理与化学两门功课的联考中，备有6到物理题，4道化学题，共10道题可供选择．要求学生从中任意选取5道作答，答对4道或5道即为良好成绩，每道题答对与否相互没有影响，设随机变量ξ为所选5道题中化学题的题数．
（1）求ξ的分布列及其均值；
（2）若学生甲随机选定了5道题，且答对任意一题的概率均为0.6，求甲没有取得良好成绩的概率．

1．若f（x）是定义在R上的连续函数，且$\lim_{x→1}\frac{f（x）}{x-1}$=2，则f（1）=（　　）

A．

2

B．

1

C．

0

D．

-1

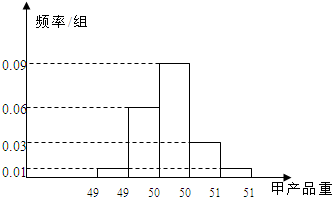20．某食品厂为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本．经统计，得到关于产品重量的样本频率分布直方图和样本频数分布表：

乙流水线 产品重量（单位：克）	频数
（490，495]	6
（495，500]	8
（500，505]	14
（505，510]	8
（510，515]	4

已知产品的重量合格标准为：重量值落在（495，510]内的产品为合格品；否则为不合格品．
（1）从甲流水线样本的合格品中任意取2件，求重量值落在（505，510]的产品件数X的分布列；
（2）从乙流水线中任取2件产品，试根据样本估计总体的思想，求其中合格品的件数Y的数学期望；
（3）从甲、乙流水线中各取2件产品，用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”，并用A表示事件“关于x的一元二次方程2x²+2ξx+ξ=0没有实数解”． 试根据样本估计总体的思想，求事件A的概率．