
科目: 来源: 题型:选择题
| A. | $\frac{3}{5}{,^{\;}}\frac{1}{2}$ | B. | $\frac{3}{5}{,^{\;}}\frac{3}{5}$ | C. | $\frac{1}{2}{,^{\;}}\frac{1}{2}$ | D. | $\frac{3}{5}{,^{\;}}\frac{2}{5}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 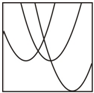 | B. | 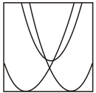 | C. | 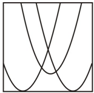 | D. |  |
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
 将边长分别为1、2、3、4、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形.由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为f(n).记数列{an}满足a1=1,an+1=$\left\{\begin{array}{l}f(n)\;\;当n为奇数\\ f({a_n})当n为偶数\end{array}$.
将边长分别为1、2、3、4、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形.由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为f(n).记数列{an}满足a1=1,an+1=$\left\{\begin{array}{l}f(n)\;\;当n为奇数\\ f({a_n})当n为偶数\end{array}$.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 证明假设n=k(k≥1且k∈N)时正确,可推出n=k+1正确 | |
| B. | 证明假设n=2k+1(k≥1且k∈N)时正确,可推出n=2k+3正确 | |
| C. | 证明假设n=2k-1(k≥1且k∈N)时正确,可推出n=2k+1正确 | |
| D. | 证明假设n≤k(k≥1且k∈N)时正确,可推出n=k+2时正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com