9．已知等比数列{a_n}满足：a₁=$\frac{1}{2}$，a₁，a₂，a₃-$\frac{1}{8}$成等差数列，公比q∈（0，1）
（1）求数列{a_n}的通项公式；
（2）设b_n=2na_n，求数列{b_n}的前n项和S_n．

8．设抛物线y²=2x的焦点为F，过点M（$\sqrt{3}$，0）的直线与抛物线相交于A，B两点，与抛物线的准线相交于C，|BF|=2，则△BCF和△ACF的面积之比为$\frac{4}{5}$．

7．已知直线l的参数方程为：$\left\{{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$（t为参数），曲线C₁的极坐标方程为：ρ=1．
（1）写出曲线C₁的直角坐标方程及其参数方程；
（2）若把曲线C₁上各点的横坐标压缩为原来的$\frac{1}{2}$倍，纵坐标压缩为原来的$\frac{{\sqrt{3}}}{2}$倍，得到曲线C₂，设点P是曲线C₂上的一个动点，求它到直线l的距离的最小值．

6．古希腊毕达哥拉斯派的数学家研究过各种多边形数，如三角形数1，3，6，10，…，第n个三角形数为$\frac{n（n+1）}{2}$=$\frac{1}{2}{n^2}$+$\frac{1}{2}$n，记第n个k边形数为N（n，k）（k≥3），以下列出了部分k边形数中第n个数的表达式：
三角形数  N（n，3）=$\frac{1}{2}{n^2}+\frac{1}{2}$n
正方形数  N（n，4）=n²
五边形数  N（n，5）=$\frac{3}{2}{n^2}-\frac{1}{2}$n
六边形数   N（n，6）=2n²-n
…
可以推测N（n，k）的表达式，由此计算N（8，12）=288．

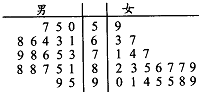5．某大学为了在2016年全国大学生成语听写大赛取得优秀成绩，抽调男女各20名学生组成集训队进行成语听写集训，集训结束时，为了检验集训效果，对所有集训队员进行成语听写考核，试题为听写100个常用成语（每个1分，满分100分），考核成绩如图茎叶图所示：
（I）若大于或等于80分为优秀队员，80分以下为非优秀队员，根据茎叶图填写下面2×2列联表，并判断能否有95%的把握认为队员的优秀与性别有关？

	非优秀	优秀	总数
男			20
女			20
总数			40

（Ⅱ）若从考核成绩95分以上（包括95分）的队员中任选两人代表这所大学参加全国大学生成语听写大赛，求至少有一名男队员参加的概率．
下面的临界值表供参考：

P（K2≥k0）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k0	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

4．已知f（x）=|x-3|-|x-a|
（1）如果f（x）＞-4的解集是R，求实数a的取值范围；
（2）如果对任意的t∈（0，1），f（x）≤$\frac{1}{t}+\frac{9}{1-t}$对x∈R恒成立，求实数a的取值范围．

3．已知函数f（x）=2ax³-3ax²+1，g（x）=-$\frac{a}{4}x+\frac{3}{2}$，若对任意给定的m∈[0，2]，关于x的方程f（x）=g（m）在区间[0，2]上总存在两个不同的解，则实数a的取值范围是（　　）

A．

（-∞，-1）

B．

（1，+∞）

C．

（-∞，-1）∪（1，+∞）

D．

[-1，1]

2．f（x）=$\left\{{\begin{array}{l}{\frac{1}{x}+alnx，（x＞0，0＜a＜e）}\\{cosx，（x≤0）}\end{array}}$，则y=f[f（x）]的零点有（　　）

A．

0个

B．

1个

C．

2个

D．

无穷多个

1．已知长方体ABCD-A₁B₁C₁D₁的所有顶点都在球O的球面上，AB=AD=1，AA₁=2，则球O的球面面积为（　　）

A．

2π

B．

4π

C．

6π

D．

24π

20．已知圆C：x²+y²+2x-3=0，直线l：x+ay+2-a=0（a∈R），则（　　）

	A．	l与C相离		B．	l与C相切
	C．	l与C相交		D．	以上三个选项均有可能