练习册

  • 练习册
  • 试题
    相关习题
     0  234763  234771  234777  234781  234787  234789  234793  234799  234801  234807  234813  234817  234819  234823  234829  234831  234837  234841  234843  234847  234849  234853  234855  234857  234858  234859  234861  234862  234863  234865  234867  234871  234873  234877  234879  234883  234889  234891  234897  234901  234903  234907  234913  234919  234921  234927  234931  234933  234939  234943  234949  234957  266669 

    科目： 来源： 题型：选择题

    10．已知函数f（x）=（2ax-lnx）x有两个极值点，则实数a的取值范围是（　　）
    A．（0，$\frac{1}{4}$）B．（0，$\frac{1}{2}$）C．（0，1）D．（0，+∞）

    查看答案和解析>>

    科目： 来源： 题型：选择题

    9．已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点，若三棱锥O-ABC体积的最大值为$\frac{4}{3}$，则球O的表面积为（　　）
    A．$\frac{32}{3}π$B．16πC．144πD．288π

    查看答案和解析>>

    科目： 来源： 题型：选择题

    8．已知椭圆的中心在原点，离心率e=$\frac{1}{2}$，且它的一个焦点与抛物线x2=-4y的焦点重合，则此椭圆的方程为（　　）
    A．$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$B．$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}=1$C．${x}^{2}+\frac{{y}^{2}}{2}=1$D．$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{8}=1$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    7．已知函数f（x）=x（lnx-ax）．
    （1）a=$\frac{1}{2}$时，求f（x）在点（1，f（1））处的切线方程；
    （2）若f（x）存在两个不同的极值x1，x2，求a的取值范围；
    （3）在（2）的条件下，求f（x）在（0，a]上的最小值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    6．如图已知椭圆C：$\frac{{x}^{2}}{4}$+y2=1，以椭圆的左顶点T为圆心作圆T：（x+2）2+y2=r2（r＞0）．设圆T与椭圆C交于点M与点N．
    （1）求$\overrightarrow{TM}$•$\overrightarrow{TN}$的最小值；
    （2）设点P是椭圆C上异于M，N的任意一点，且直线MP，NP分别与x轴交于点R，S，O为坐标原点，求证：丨OR丨•丨OS丨为定值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    5．已知函数$f（x）=\frac{1}{3}{x^3}+（{a-6}）x$，g（x）=-x2+lnx-1
    （Ⅰ）若a=2，求f（x）的单调区间；
    （Ⅱ）对?x1，x2∈[1，+∞），都有f（x1）＞g（x2），求实数a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    4．某地区在对人们休闲方式的一次调查中，共调查了120人，其中女性70人，男性50人．女性中有40人主要的休闲方式是看电视，另外30人主要的休闲方式是运动；男性中有20人主要的休闲方式是看电视，另外30人主要的休闲方式是运动．
    （1）根据以上数据建立一个2×2列联表；
    （2）能否在犯错误的概率不超过0.025的前提下认为“性别与休闲方式有关系”？
    附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
    P（K2≥k）0.100.0500.0250.0100.0050.001
    k2.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目： 来源： 题型：选择题

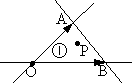    3．如图，已知O，A，B是平面内不共线的三点，且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$，直线OA，OB，AB将平面区域分成7部分，若点P落在区域①中（含边界），则z=2x+y的最大值为（　　）
    A．不存在B．0C．1D．2

    查看答案和解析>>

    科目： 来源： 题型：选择题

    2．如图给出一个“三角形数阵”，已知每一列的数成等差数列，从第三行起，每一行的数成等比数列，每一行的公比都相等，记第i行第j列的数为${a_{ij}}（i≥j，i，j∈{N^*}）$，则a63=（　　）
    A．$\frac{1}{8}$B．$\frac{1}{4}$C．$\frac{1}{2}$D．1

    查看答案和解析>>

    科目： 来源： 题型：解答题

    1．在平面直角坐标系xOy中，曲线${C_1}：{（x-2）^2}+{（y-2）^2}=8$，曲线${C_2}：{x^2}+{y^2}={r^2}（0＜r＜4）$，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，射线θ=α$（0＜α＜\frac{π}{2}）$与曲线C1交于O，P两点，与曲线C2交于O，N两点，且|PN|最大值为$2\sqrt{2}$
    （1）将曲线C1与曲线C2化成极坐标方程，并求r的值；
    （2）射线$θ=α+\frac{π}{4}$与曲线C1交于O，Q两点，与曲线C2交于O，M两点，求四边形MNPQ面积的最大值．

    查看答案和解析>>

    同步练习册答案