14．已知圆F1:2+y2=16.圆心为F1.定点F2.P为圆F1上一点.线段PF2的垂直平分线与直线PF1交于点Q．(1)求点Q的轨迹C的方程,的直线l与曲线C交于不同的两点A和B.且满足∠AOB＜——青夏教育精英家教网—

相关习题

0 234839 234847 234853 234857 234863 234865 234869 234875 234877 234883 234889 234893 234895 234899 234905 234907 234913 234917 234919 234923 234925 234929 234931 234933 234934 234935 234937 234938 234939 234941 234943 234947 234949 234953 234955 234959 234965 234967 234973 234977 234979 234983 234989 234995 234997 235003 235007 235009 235015 235019 235025 235033 266669

科目： 来源： 题型：解答题

14．已知圆F₁：（x+$\sqrt{3}$）²+y²=16，圆心为F₁，定点F₂（$\sqrt{3}$，0），P为圆F₁上一点，线段PF₂的垂直平分线与直线PF₁交于点Q．
（1）求点Q的轨迹C的方程；
（2）过点（0，2）的直线l与曲线C交于不同的两点A和B，且满足∠AOB＜90°（O为坐标原点），求直线l斜率的取值范围．

查看答案和解析>>

科目： 来源： 题型：解答题

13．

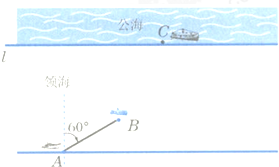设直线l为公海的分界线，一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船，走私船正向停泊在公海上接应的走私海轮C航行，以便上海轮后逃窜．已知巡逻艇的航速是走私船航速的2倍，A与公海相距约为20海里，走私船可能向任一方向逃窜，请回答下列问题：
（1）如果走私船和巡逻艇都是沿直线航行，那么走私船能被截获的点是哪些？
（2）根据截获点的轨迹，探讨“可截获区域”和“非截获区域”．

查看答案和解析>>

科目： 来源： 题型：解答题

12．

已知四棱锥P-ABCD，底面ABCD是∠A=60°的菱形，又PD⊥底面ABCD，且PD=CD，点M、N分别是棱AD、PC的中点．
（Ⅰ）证明：DN∥平面PMB；
（Ⅱ）求二面角P-AB-D的余弦值．

查看答案和解析>>

科目： 来源： 题型：解答题

11．

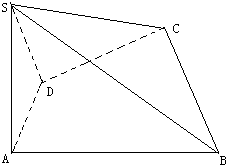如图四棱锥S-ABCD，底面四边形ABCD满足条件∠DAB=90°，∠ADC=135°，AB=5，CD=2$\sqrt{2}$，AD=2，侧面SAD垂直于底面ABCD，SA=2，
（1）若SB上存在一点E，使得CE∥平面SAD，求$\frac{SE}{SB}$的值；
（2）求此四棱锥体积的最大值；
（3）当体积最大时，求二面角A-SC-B大小的余弦值．

查看答案和解析>>

科目： 来源： 题型：解答题

10．已知函数f（x）=x³+$\frac{5}{2}$x²+ax+b（a，b为常数），其图象是曲线C．
（1）当a=-2时，求函数f（x）的单调减区间；
（2）设函数f（x）的导函数为f′（x），若存在唯一的实数x₀，使得f（x₀）=x₀与f′（x₀）=0同时成立，求实数b的取值范围．

查看答案和解析>>

科目： 来源： 题型：填空题

9．已知向量$\overrightarrow a$，$\overrightarrow b$满足|$\overrightarrow a$|=2|$\overrightarrow b$|≠0，且函数在f（x）=$\frac{1}{3}{x^3}+\frac{1}{2}|\overrightarrow a|{x^2}$$+（\overrightarrow a•\overrightarrow b）x$在R上有极值，则向量$\overrightarrow a$，$\overrightarrow b$的夹角的取值范围是（$\frac{π}{3}$，π）．

查看答案和解析>>

科目： 来源： 题型：解答题

8．已知函数f（x）=lnx-ax-3（a≠0）
（1）求函数f（x）的极值；
（2）若对于任意的a∈[1，2]，若函数g（x）=x³+$\frac{{x}^{2}}{2}$[m-2f′（x）]在区间（a，3）上有最值，求实数m的取值范围．

查看答案和解析>>

科目： 来源： 题型：解答题

7．设f（x）=x-alnx．（a≠0）
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）若f（x）≥a²，求a的取值范围．

查看答案和解析>>

科目： 来源： 题型：选择题

6．已知函数f（x）=lnx-（$\frac{1}{2}$）^x+1，则不等式f（2x-3）＜$\frac{1}{2}$的解集为（　　）

A．

{x|{$\frac{3}{2}$＜x＜2}

B．