
科目: 来源: 题型:选择题
| A. | 5$\sqrt{21}$m | B. | 10m | C. | $\frac{4900}{13}$m | D. | 35m |
查看答案和解析>>
科目: 来源: 题型:解答题
 在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,其焦点与椭圆上最近点的距离为2-$\sqrt{2}$.
在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,其焦点与椭圆上最近点的距离为2-$\sqrt{2}$.查看答案和解析>>
科目: 来源: 题型:解答题
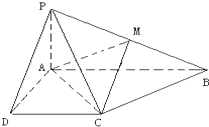 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.查看答案和解析>>
科目: 来源: 题型:解答题
 二十世纪50年代,日本熊本县水俣市的许多居民都患了运动失调、四肢麻木等症状,人们把它称为水俣病.经调查发现一家工厂排出的废水中含有甲基汞,使鱼类受到污染.人们长期食用含高浓度甲基汞的鱼类引起汞中毒. 引起世人对食品安全的关注.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.00ppm.罗非鱼是体型较大,生命周期长的食肉鱼,其体内汞含量比其他鱼偏高.现从一批罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前一位数字为茎,小数点后一位数字为叶)如下:
二十世纪50年代,日本熊本县水俣市的许多居民都患了运动失调、四肢麻木等症状,人们把它称为水俣病.经调查发现一家工厂排出的废水中含有甲基汞,使鱼类受到污染.人们长期食用含高浓度甲基汞的鱼类引起汞中毒. 引起世人对食品安全的关注.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.00ppm.罗非鱼是体型较大,生命周期长的食肉鱼,其体内汞含量比其他鱼偏高.现从一批罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前一位数字为茎,小数点后一位数字为叶)如下:查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为棱DD1上一点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为棱DD1上一点.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com