3．已知函数f（x）=$\left\{{\begin{array}{l}{sin\frac{πx}{2}，x≤0}\\{\frac{1}{6}-{{log}_3}x，x＞0}\end{array}}$，则$f[{f（{3\sqrt{3}}）}]$=-$\frac{\sqrt{3}}{2}$．

2．已知公比小于1的等比数列{a_n}的前n项和为S_n，a₁=$\frac{1}{2}，7{a_2}=2{S_3}$．
（1）求数列{a_n}的通项公式；
（2）设b_n=log₂（1-S_n+1），若$\frac{1}{{{b_1}{b_3}}}+\frac{1}{{{b_3}{b_5}}}+…+\frac{1}{{{b_{2n-1}}{b_{2n+1}}}}=\frac{5}{21}$，求n．

1．已知等比数列{a_n}共有10项，其中奇数项之积为2，偶数项之积为64，则其公比是（　　）

A．

$\frac{3}{2}$

B．

$\sqrt{2}$

C．

2

D．

$2\sqrt{2}$

20．若函数y=sin（2x+φ）（0＜φ＜π）的图象关于直线x=$\frac{π}{3}$对称，则φ的值为$\frac{5π}{6}$．

19．在△ABC中，a，b，c分别是角A，B，C所对边的边长，若cosC+sinC-$\frac{2}{cosB+sinB}$=0，则$\frac{a+b}{c}$的值是（　　）

A．

$\sqrt{2}$-1

B．

$\sqrt{2}$+1

C．

$\sqrt{3}$+1

D．

2

18．函数f（x）=sin（ωx+φ）（其中ω＞0且|φ|≤$\frac{π}{2}$）的图象如图所示，为了得到y=sinωx的图象，只需把y=f（x）的图象上所有点（　　）

	A．	向右平移$\frac{π}{6}$个单位长度		B．	向右平移$\frac{π}{3}$个单位长度
	C．	向左平移$\frac{π}{6}$个单位长度		D．	向左平移$\frac{π}{3}$个单位长度

17．下列命题正确的是（　　）

	A．	命题?x0∈R，x${\;}_{0}^{2}$+1＞3x0的否定是：?x∈R，x2+1＜3x
	B．	命题△ABC中，若A＞B，则cosA＞cosB的否命题是真命题
	C．	平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是钝角的充要条件是：$\overrightarrow{a}$•$\overrightarrow{b}$＜0
	D．	ω=1是函数f（x）=sinωx-cosωx的最小正周期为2π的充分不必要条件

16．已知函数f（x）=$\frac{1}{2}a{x^2}$+2x-lnx．
（1）若a=-$\frac{3}{4}$，判断函数f（x）的单调性；
（2）若函数f（x）在定义域内单调递减，求实数a的取值范围；
（3）当a=-$\frac{1}{2}$时，关于x的方程f（x）=$\frac{1}{2}$x-b在[1，4]上恰有两个不相等的实数根，求实数b的取值范围．

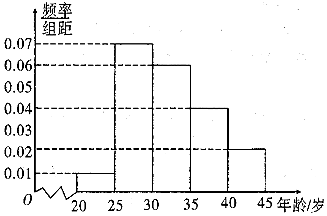15．“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称，某市为了了解人们对“一带一路”的认知程度，对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛，满分100分（90分及以上为认知程度高），现从参赛者中抽取了x人，按年龄分成5组（第一组：[20，25），第二组：[25，30），第三组：[30，35），第四组：[35，40），第五组：[40，45]），得到如图所示的频率分布直方图，已知第一组有6人．
（1）求x；
（2）求抽取的x人的年龄的中位数（结果保留整数）；
（3）从该市大学生、军人、医务人员、工人、个体户五种人中用分层抽样的方法依次抽取6人，42人，36人，24人，12人，分别记1～5组，从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛代表相应的成绩，年龄组中1～5组的成绩分别为93，96，97，94，90，职业组中1～5组的成绩分别为93，98，94，95，90．
（I）分别求5个年龄组和5个职业组成绩的平均数和方差；
（II）以上述数据为依据，评价5个年龄组和5个职业组对“一带一路”的认知程度，并谈谈你的感想．

14．设数列{a_n}为等差数列，且a₁₁=$\frac{3π}{8}$，若f（x）=sin2x+2cos²x，记b_n=f（a_n），则数列{b_n}的前21项和为21．