练习册

  • 练习册
  • 试题
    相关习题
     0  235203  235211  235217  235221  235227  235229  235233  235239  235241  235247  235253  235257  235259  235263  235269  235271  235277  235281  235283  235287  235289  235293  235295  235297  235298  235299  235301  235302  235303  235305  235307  235311  235313  235317  235319  235323  235329  235331  235337  235341  235343  235347  235353  235359  235361  235367  235371  235373  235379  235383  235389  235397  266669 

    科目： 来源： 题型：解答题

    11．已知二次函数f（x）=ax2-4x+c的值域为[0，+∞）．
    （1）判断此函数的奇偶性，并说明理由；
    （2）判断此函数在[$\frac{2}{a}$，+∞）的单调性，并用单调性的定义证明你的结论；
    （3）求出f（x）在[1，+∞）上的最小值g（a），并求g（a）的值域．

    查看答案和解析>>

    科目： 来源： 题型：解答题

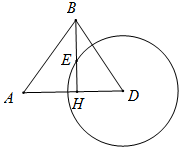    10．如图，我海监船在D岛海域例行维权巡航，某时刻航行至A处，此时测得其北偏东30°方向与它相距20海里的B处有一外国船只，且D岛位于海监船正东18海里处．
    （1）求此时该外国船只与D岛的距离；
    （2）观测中发现，此外国船只正以每小时4海里的速度沿正南方航行．为了将该船拦截在离D岛12海里的E处（E在B的正南方向），不让其进入D岛12海里内的海域，试确定海监船的航向，并求其速度的最小值（角度精确到0.1°，速度精确到0.1海里/小时）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    9．在正三棱锥P-ABC中，已知底面等边三角形的边长为6，侧棱长为4．
    （1）求证：PA⊥BC；
    （2）求此三棱锥的全面积和体积．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    8．定义f（x）={x}（其中{x}表示不小于x的最小整数）为“取上整函数”，例如{2.1}=3，{4}=4．以下关于“取上整函数”性质的描述，正确的是（　　）
    ①f（2x）=2f（x）；                         
    ②若f（x1）=f（x2），则x1-x2＜1；
    ③任意x1，x2∈R，f（x1+x2）≤f（x1）+f（x2）；
    ④$f（x）+f（x+\frac{1}{2}）=f（2x）$．
    A．①②B．①③C．②③D．②④

    查看答案和解析>>

    科目： 来源： 题型：选择题

    7．如图，在圆C中，点A、B在圆上，则$\overrightarrow{AB}•\overrightarrow{AC}$的值（　　）
    A．只与圆C的半径有关
    B．既与圆C的半径有关，又与弦AB的长度有关
    C．只与弦AB的长度有关
    D．是与圆C的半径和弦AB的长度均无关的定值

    查看答案和解析>>

    科目： 来源： 题型：选择题

    6．已知函数$f（x）=sin（2x+\frac{π}{3}）$在区间[0，a]（其中a＞0）上单调递增，则实数a的取值范围是（　　）
    A．$0＜a≤\frac{π}{2}$B．$0＜a≤\frac{π}{12}$
    C．$a=kπ+\frac{π}{12}，k∈{N^*}$D．$2kπ＜a≤2kπ+\frac{π}{12}，k∈N$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    5．在空间，α表示平面，m，n表示二条直线，则下列命题中错误的是（　　）
    A．若m∥α，m、n不平行，则n与α不平行B．若m∥α，m、n不垂直，则n与α不垂直
    C．若m⊥α，m、n不平行，则n与α不垂直D．若m⊥α，m、n不垂直，则n与α不平行

    查看答案和解析>>

    科目： 来源： 题型：填空题

    4．当实数x，y满足x2+y2=1时，|x+2y+a|+|3-x-2y|的取值与x，y均无关，则实数a的取范围是[$\sqrt{5}$，+∞）．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    3．点M（20，40），抛物线y2=2px（p＞0）的焦点为F，若对于抛物线上的任意点P，|PM|+|PF|的最小值为41，则p的值等于42或22．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    2．设函数f（x）=$\left\{\begin{array}{l}{{x}^{6}，x≥1}\\{-2x-1，x≤-1}\end{array}\right.$，则当x≤-1时，则f[f（x）]表达式的展开式中含x2项的系数是60．

    查看答案和解析>>

    同步练习册答案