练习册

  • 练习册
  • 试题
    相关习题
     0  235386  235394  235400  235404  235410  235412  235416  235422  235424  235430  235436  235440  235442  235446  235452  235454  235460  235464  235466  235470  235472  235476  235478  235480  235481  235482  235484  235485  235486  235488  235490  235494  235496  235500  235502  235506  235512  235514  235520  235524  235526  235530  235536  235542  235544  235550  235554  235556  235562  235566  235572  235580  266669 

    科目： 来源： 题型：填空题

    7．两直线l1：2x+y-6=0，l2：x-y-6=0的交点P与圆（x-5）2+（y-5）2=4上任一点Q连线的中点的轨迹方程是（x-$\frac{9}{2}$）2+（y-$\frac{3}{2}$）2=1．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    6．已知关于x的不等式组$\left\{\begin{array}{l}{4（x-1）+2＞3x}\\{x-1＜\frac{6x+a}{7}}\end{array}\right.$，有且只有三个整数解，则a的取值范围是（　　）
    A．-2≤a≤-1B．-2≤a＜-1C．-2＜a≤-1D．-2＜a＜-1

    查看答案和解析>>

    科目： 来源： 题型：解答题

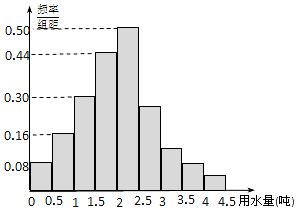    5．某地区100位居民的人均月用水量（单位：t）的频率分布直方图及频数分布表如下：
    分组频数
    [0，0.5）4
    [0.5，1）8
    [1，1.5）15
    [1.5，2）22
    [2，2.5）25
    [2.5，3）14
    [3，3.5）6
    [3.5，4）4
    [4，4.5）2
    合计100
    （1）根据频率分布直方图估计这组数据的众数与平均数；
    （2）当地政府制定了人均月用水量为3t的标准，若超出标准加倍收费，当地政府解释说，85%以上的居民不超出这个标准，这个解释对吗？为什么？

    查看答案和解析>>

    科目： 来源： 题型：选择题

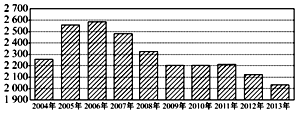    4．我国一直为“低碳生活”努力，根据下面给出的2004年至2013年我国某有害物质排放量（单位：万吨）柱形图，以下结论正确的是（　　）
    A．逐年比较，2005年减少二氧化硫排放量的效果最显著
    B．2008年我国治理二氧化硫排放显现成效
    C．2006年以来我国二氧化硫年排放量呈减少趋势
    D．2006年以来我国二氧化硫年排放量与年份正相关

    查看答案和解析>>

    科目： 来源： 题型：解答题

    3．若（3x-1）55=a0+a1x+…+a55x55，求|a1|+|a2|+…+|a55|．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    2．设数列{an}是等差数列，数列{bn}是首项为-$\frac{1}{100}$的等比数列，且$\frac{{b}_{6}}{{b}_{7}}$=$\frac{1}{2}$，10a1•b2=-1，2a1•b2+5a2•b3=-2
    （1）求数列{an}，{bn}的通项公式；
    （2）求数列{an+$\frac{1}{{b}_{n}}$}的前n项和Sn；
    （3）求Sn的最小值．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    1．M是△ABC所在平面内一点，$\frac{2}{3}\overrightarrow{MB}+\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow 0$，D为AC中点，则$\frac{{|\overrightarrow{MD}|}}{{|\overrightarrow{BM}|}}$的值为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．1D．2

    查看答案和解析>>

    科目： 来源： 题型：解答题

    20．已知等差数列{an}的首项为c，公差为d，等比数列{bn}的首项为d，公比为c，其中c，d∈Z，且a1＜b1＜a2＜
    b2＜a3．
    （1）求证：0＜c＜d，并由b2＜a3推导c的值；
    （2）若数列{an}共有3n项，前n项的和为A，其后的n项的和为B，再其后的n项的和为C，求$\frac{{B}^{2}-AC}{（A-C）^{2}}$的比值．
    （3）若数列{bn}的前n项，前2n项、前3n项的和分别为D，G，H，试用含字母D，G的式子来表示H（即H=f（D，G），且不含字母d）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    19．设函数f（x）=lnx，g（x）=lnx-x+2．
    （1）求函数g（x）的极大值；
    （2）若关于x的不等式$mf（x）≥\frac{x-1}{x+1}$在[1，+∞）上恒成立，求实数m的取值范围；
    （3）已知$α∈（0，\frac{π}{2}）$，试比较f（tanα）与-cos2α的大小，并说明理由．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    18．若函数f（x）=x3-ax2-x+6在（0，1）上单调递减，则实数a取值范围是（　　）
    A．a=1B．a≥1C．a≤1D．0＜a＜1

    查看答案和解析>>

    同步练习册答案