17．设命题P：?x∈R，x²+2＞0．则￢P为（　　）

	A．	$?{x_0}∈R，{x_0}^2+2＞0$		B．	$?{x_0}∈R，{x_0}^2+2≤0$
	C．	$?{x_0}∈R，{x_0}^2+2＜0$		D．	?x∈R，x2+2≤0

16．在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ²-2ρcosθ-4ρsinθ+4=0，直线l的方程为x-y-1=0．
（1）写出曲线C的参数方程；
（2）在曲线C上求一点P，使点P到直线l的距离最大，并求出此最大值．

15．设函数$f（x）=\frac{1}{2}{x^2}-（a+1）x+alnx，a＞0$．
（1）求函数f（x）的单调区间；
（2）讨论函数f（x）的零点个数．

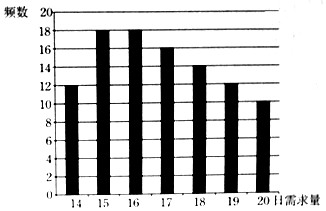14．某蛋糕店每天制作生日蛋糕若干个，每个生日蛋糕成本为50元，每个蛋糕的售价为100元，如果当天卖不完，剩余的蛋糕作垃圾处理．现搜集并整理了100天生日蛋糕的日需求量（单位：个），得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率．
（1）若该蛋糕店某一天制作生日蛋糕17个，设当天的需求量为n（n∈N），则当天的利润y（单位：元）是多少？
（2）若蛋糕店一天制作17个生日蛋糕．
①求当天的利润y（单位：元）关于当天需求量n的函数解析式；
②求当天的利润不低于600圆的概率．
（3）若蛋糕店计划一天制作16个或17个生日蛋糕，请你以蛋糕店一天利润的平均值作为决策依据，应该制作16个还是17个生日蛋糕？

13．已知如图正四面体SABC的侧面积为$48\sqrt{3}$，O为底面正三角形ABC的中心．
（1）求证：SA⊥BC；
（2）求点O到侧面SABC的距离．

12．已知{a_n}是等差数列，满足a₁=1，a₄=-5，数列{b_n}满足b₁=1，b₄=21，且{a_n+b_n}为等比数列．
（1）求数列{a_n}和{b_n}的通项公式；
（2）求数列{b_n}的前n项和S_n．

11．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}（x+2），x≥1}\\{{e}^{x}-1，x＜1}\end{array}\right.$，若m＞0，n＞0，且m+n=f[f（ln2）]，则$\frac{1}{m}+\frac{2}{n}$的最小值为3+2$\sqrt{2}$．

10．已知θ为第二象限角，且$tan（θ-\frac{π}{4}）=3$，则sinθ+cosθ=$\frac{{\sqrt{5}}}{5}$．

9．一个几何体的三视图如图所示，正视图和侧视图是两个全等的三角形，俯视图是$\frac{3}{4}$个圆，则该几何体的体积等于9π．

8．已知三棱柱ABC-A₁B₁C₁的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为$2\sqrt{3}$，AB=2，AC=1，∠BAC=60°，则此球的表面积等于（　　）

A．

5π

B．

20π

C．

8π

D．

16π