11．我国古代数学著作《九章算术》有如下问题：“今有金箠，长五尺，斩本一尺，重四斤，斩末一尺，重二斤，问次一尺各重几何？”意思是：“现有一根金箠，长五尺，一头粗，一头细，在粗的一端截下1尺，重4斤；在细的一端截下1尺，重2斤；问依次每一尺各重多少斤？”根据上题的已知条件，若金箠由粗到细是均匀变化的，问第二尺与第四尺的重量之和为（　　）

A．

6 斤

B．

9 斤

C．

9.5斤

D．

12 斤

10．已知△ABC的面积为$\sqrt{3}$，且∠C=30°，BC=2$\sqrt{3}$，则AB等于（　　）

A．

1

B．

$\sqrt{3}$

C．

2

D．

2$\sqrt{3}$

9．在{1，3，5}和{2，4}两个集合中各取一个数组成一个两位数，则这个数能被4整除的概率是（　　）

A．

$\frac{1}{3}$

B．

$\frac{1}{2}$

C．

$\frac{1}{6}$

D．

$\frac{1}{4}$

8．设n∈N^*，n≥3，k∈N^*．
（1）求值：
①kC_n^k-nC_n-1^k-1；
②k²C_n^k-n（n-1）C_n-2^k-2-nC_n-1^k-1（k≥2）；
（2）化简：1²C_n⁰+2²C_n¹+3²C_n²+…+（k+1）²C_n^k+…+（n+1）²C_nⁿ．

7．某年级星期一至星期五每天下午排3节课，每天下午随机选择1节作为综合实践课（上午不排该课程），张老师与王老师分别任教甲、乙两个班的综合实践课程．
（1）求这两个班“在星期一不同时上综合实践课”的概率；
（2）设这两个班“在一周中同时上综合实践课的节数”为X，求X的概率分布表与数学期望E（X）．

6．若实数x，y，z满足x+2y+z=1，求x²+y²+z²的最小值．

5．在平面直角坐标系xOy中，已知直线$l：\left\{\begin{array}{l}x=\frac{3}{5}t\\ y=\frac{4}{5}t\end{array}\right.（t$为参数）．现以坐标原点O为极点，以x轴非负半轴为极轴建立极坐标系，设圆C的极坐标方程为ρ=2cosθ，直线l与圆C交于A，B两点，求弦AB的长．

4．如图，AB是半圆O的直径，点P为半圆O外一点，PA，PB分别交半圆O于点D，C．若AD=2，PD=4，PC=3，求BD的长．

3．若存在常数k（k∈N^*，k≥2）、q、d，使得无穷数列{a_n}满足${a_{n+1}}=\left\{\begin{array}{l}{a_n}+d，\frac{n}{k}∉{N^*}\\ q{a_n}，\frac{n}{k}∈{N^*}\end{array}\right.$则称数列{a_n}为“段比差数列”，其中常数k、q、d分别叫做段长、段比、段差．设数列{b_n}为“段比差数列”．
（1）若{b_n}的首项、段长、段比、段差分别为1、3、q、3．
①当q=0时，求b₂₀₁₆；
②当q=1时，设{b_n}的前3n项和为S_3n，若不等式${S_{3n}}≤λ•{3^{n-1}}$对n∈N^*恒成立，求实数λ的取值范围；
（2）设{b_n}为等比数列，且首项为b，试写出所有满足条件的{b_n}，并说明理由．

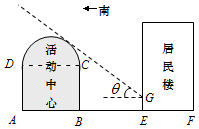2．如图所示，某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心，其中AE=30米．活动中心东西走向，与居民楼平行．从东向西看活动中心的截面图的下部分是长方形ABCD，上部分是以DC为直径的半圆．为了保证居民楼住户的采光要求，活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米，其中该太阳光线与水平线的夹角θ满足$tanθ=\frac{3}{4}$．
（1）若设计AB=18米，AD=6米，问能否保证上述采光要求？
（2）在保证上述采光要求的前提下，如何设计AB与AD的长度，可使得活动中心的截面面积最大？（注：计算中π取3）