1．已知函数$f（x）=\frac{1+a}{x}（a∈R）$．
（Ⅰ） 当a=0时，求曲线f （x）在x=1处的切线方程；
（Ⅱ） 设函数h（x）=alnx-x-f（x），求函数h （x）的极值；
（Ⅲ） 若g（x）=alnx-x在[1，e]（e=2.718 28…）上存在一点x₀，使得g（x₀）≥f（x₀）成立，求a的取值范围．

20．已知定点Q（$\sqrt{3}$，0），P为圆N：${（x+\sqrt{3}）^2}+{y^2}=24$上任意一点，线段QP的垂直平分线交NP于点M．
（Ⅰ）当P点在圆周上运动时，求点M （x，y） 的轨迹C的方程；
（Ⅱ）若直线l与曲线C交于A、B两点，且$\overrightarrow{OA}•\overrightarrow{OB}=0$，求证：直线l与某个定圆E相切，并求出定圆E的方程．

19．随着社会的发展，终身学习成为必要，工人知识要更新，学习培训必不可少，现某工厂有工人1000名，其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训（称为B类工人），从该工厂的工人中共抽查了100名工人，调查他们的生产能力（此处生产能力指一天加工的零件数）得到A类工人生产能力的茎叶图（图1），B类工人生产能力的频率分布直方图（图2）．

（Ⅰ）问A类、B类工人各抽查了多少工人，并求出直方图中的x；
（Ⅱ）求A类工人生产能力的中位数，并估计B类工人生产能力的平均数（同一组中的数据用该组区间的中点值作代表）；
（Ⅲ） 若规定生产能力在[130，150]内为能力优秀，由以上统计数据在答题卡上完成下面的2×2列联表，并判断是否可以在犯错误概率不超过0.1%的前提下，认为生产能力与培训时间长短有关．
能力与培训时间列联表

	短期培训	长期培训	合计
能力优秀	8	54	62
能力不优秀	17	21	38
合计	25	75	100

参考数据：

P（K2≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．

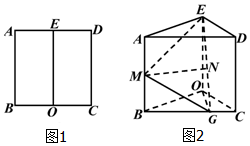18．如图1，在边长为$2\sqrt{3}$的正方形ABCD中，E、O分别为 AD、BC的中点，沿 EO将矩形ABOE折起使得∠BOC=120°，如图2，点G 在BC上，BG=2GC，M、N分别为AB、EG中点．
（Ⅰ）求证：OE⊥MN；
（Ⅱ）求点M到平面OEG的距离．

17．在等差数列{a_n}中，a₂=4，前4项之和为18．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设${b_n}=n•{2^{{a_n}-2}}$，求数列{b_n}的前n项和T_n．

16．过球O表面上一点A引三条长度相等的弦AB，AC，AD，且两两夹角都为60°，若球半径为R，则△BCD的面积为$\frac{2\sqrt{3}}{3}{R}^{2}$．

15．已知直线x-2y+2=0与圆C相切，圆C与x轴交于两点A （-1，0）、B （3，0），则圆C的方程为（x-1）²+（y+1）²=5或（x-1）²+（y+11）²=125．

14．若α∈（0，π），且sin2α+2cos2α=2，则tanα=$\frac{1}{2}$．

13．已知F₁，F₂分别是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1（a，b＞0）$的两个焦点，过其中一个焦点与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M，若点M在以线段F₁F₂为直径的圆内，则双曲线离心率的取值范围是（　　）

A．

（1，2）

B．

（2，+∞）

C．

$（1，\;\sqrt{2}）$

D．

$（\sqrt{2}，\;+∞）$

12．已知函数$f（x）=3cos（ωx+\frac{π}{3}）（ω＞0）$和g（x）=2sin（2x+φ）+1的图象的对称轴完全相同，若$x∈[0，\frac{π}{3}]$，则f（x）的取值范围是（　　）

A．

[-3，3]

B．

$[-\frac{3}{2}，3]$

C．

$[-3，\frac{{3\sqrt{3}}}{2}]$

D．

$[-3，\frac{3}{2}]$