3．已知集合A={x|（x+2）（x-3）＜0}，则A∩N（N为自然数集）为（　　）

A．

（-∞，-2）∪（3，+∞）

B．

（2，3）

C．

{0，1，2}

D．

{1，2}

2．设函数f（x）=e^x-ax²+1，曲线y=f（x）在x=1处的切线方程为y=bx+2．
（1）求a，b的值；
（2）若方程F（x）=f（x）-mx有两个极值点x₁，x₂（x₁＜x₂），x₀是x₁与x₂的等差中项；
（i）求实数m的取值范围；
（ii）求证：f′（x₀）＜0 （ f′（x）为f（x）的导函数）．

1．已知椭圆C_n：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=n（a＞b＞1，n∈N^*），F₁，F₂是椭圆C₄的焦点，A（2，$\sqrt{2}$）是椭圆C₄上一点，且$\overrightarrow{A{F}_{2}}$?$\overrightarrow{{F}_{1}{F}_{2}}$=0；
（1）求C_n的离心率并求出C₁的方程；
（2）P为椭圆C₂上任意一点，直线PF₁交椭圆C₄于点E，F，直线PF₂交椭圆C₄于点M，N，设直线PF₁的斜率为k₁，直线PF₂的斜率为k₂；
（i）求证：k₁k₂=-$\frac{1}{2}$    
（ii）求|MN|?|EF|的取值范围．

20．自主招生，是高校选拔录取工作改革的重要环节，通过高考自主招生笔试和面试之后，可以得到相应的高考降分政策；某高中高一学生共有1000人，其中城填初中毕业生750名（称为“城填生“），农村初中毕业生250人（称为“农村生“）；为了摸清学生是否愿意参加自主招生，以便安排自主招生培训，拟采用分层抽样的方法抽取100名学生进行调查；
（1）试完成下列2×2联表，并分析是否有95%以上的把握说“是否愿意参加自主招生“与生源有关．

	愿意参加	不愿意参加	合计
城填生	50	25	75
农村生	10	15	25
合计	60	40	100

（2）现对愿意参加自主招生的同学组织摸底考试，考试题共有5道题，每题20分，对于这5道题，考生“高富帅”完全会答的有3道，不完全会的有2道，不完全会的每道题她得分S的概率满足：SKIPIF 1＜0，假设解答各题之间没有影响．
①对于一道不完全会的题，求“高富帅”得分的均值E（s）；
②试求“高富帅”在本次摸底考试中总得分的数学期望．
参考数据：

P（K2≥k0）	0.10	0.05	0.025	0.010	0.005	0.001
k0	2.706	3.841	5.024	6.635	7.879	10.828

K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d）

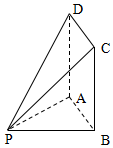19．如图，四边形ABCD为矩形，PB=20，BC=30，PA⊥平面ABCD．
（1）证明：平面PCD⊥平面PAD；
（2）当AB的长为多少时，面PAB与面PCD所成的二面角为60°？请说明理由．

18．等比数列{a_n}的各项均为正数，且a₁+2a₂=1，a₃²=4a₂a₆．
（1）求数列{a_n}的通项公式；
（2）设b_n+2=3log₂$\frac{1}{{a}_{n}}$，求数列{a_nb_n}的前n项和．

17．若二次函数f（x）=x²+1的图象与曲线C：g（x）=ae^x+1（a＞0）存在公共切线，则实数a的取值范围为（0，$\frac{4}{{e}^{2}}$]．

16．在△ABC中，角A，B，C所对的边分别为a，b，c，且2bcosC-3ccosB=a，则tan（B-C）的最大值为$\frac{3}{4}$．

15．已知α，β是两个不同的平面，l，m是两条不同直线，l⊥α，m?β．给出下列命题：
①α∥β⇒l⊥m；②α⊥β⇒l∥m；③m∥α⇒l⊥β；  ④l⊥β⇒m∥α．
其中正确的命题是①④． （填写所有正确命题的序号）．

14．若a=2，则（1+ax）⁵的展开式中x³项的系数为80．