13．若函数f（x）=x²+$\frac{a-1}{x}$为偶函数，则实数a=1．

12．若x＞0，则函数f（x）=$\frac{2}{x}$+x的最小值为2$\sqrt{2}$．

11．已知A={x|x≤7}，B={x|x＞2}，则A∩B={x|2＜x≤7}．

10．已知圆C过点$A（\frac{3}{4}，\;0）$，且与直线$l：\;x=-\frac{3}{4}$相切，
（I）求圆心C的轨迹方程；
（II） O为原点，圆心C的轨迹上两点M、N（不同于点O）满足$\overrightarrow{OM}•\overrightarrow{ON}=0$，已知$\overrightarrow{OP}=\frac{1}{3}\overrightarrow{OM}$，$\overrightarrow{OQ}=\frac{1}{3}\overrightarrow{ON}$，证明直线PQ过定点，并求出该定点坐标和△APQ面积的最小值．

9．某次数学测验后，数学老师统计了本班学生对选做题的选做情况，得到如表数据：（单位：人）

	坐标系与参数方程	不等式选讲	合计
男同学	22	8	30
女同学	8	12	20
合计	30	20	50

（I）请完成题中的2×2列联表；并根据表中的数据判断，是否有超过97.5%的把握认为选做“坐标系与参数方程”或“不等式选讲”与性别有关？
（II）经过多次测试后，甲同学发现自己解答一道“坐标系与参数方程”所用的时间为区间[5，7]内一个随机值（单位：分钟），解答一道“不等式选讲”所用的时间为区间[6，8]内一个随机值（单位：分钟），试求甲在考试中选做“坐标系与参数方程”比选做“不等式选讲”所用时间更长的概率．
附表及公式：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$

P（K2≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

8．如图，在四棱锥P-ABCD中，O∈AD，AD∥BC，AB⊥AD，AO=AB=BC=1，PO=$\sqrt{2}$，$PC=\sqrt{3}$．
（I）证明：平面POC⊥平面PAD；
（II）若CD=$\sqrt{2}$，三棱锥P-ABD与C-PBD的体积分别为V₁、V₂，求证V₁=2V₂．

7．已知递增数列{a_n}的前n项和为S_n，且满足$2{S_n}=a_n^2+n$．
（I）求a_n；
（II）设${b_n}={a_{n+1}}•{2^n}$，求数列{b_n}的前n项和T_n．

6．直线l：x+4y=2与圆C：x²+y²=1交于A、B两点，O为坐标原点，若直线OA、OB的倾斜角分别为α、β，则cosα+cosβ=$\frac{4}{17}$．

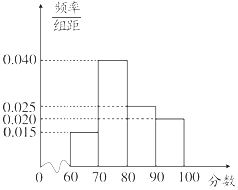5．2016年年底，某商业集团根据相关评分标准，对所属20家商业连锁店进行了年度考核评估，并依据考核评估得分（最低分60分，最高分100分）将这些连锁店分别评定为A，B，C，D四个类型，其考核评估标准如表：

评估得分	[60，70）	[70，80）	[80，90）	[90，100]
评分类型	D	C	B	A

考核评估后，对各连锁店的评估分数进行统计分析，得其频率分布直方图如下：
（Ⅰ）评分类型为A的商业连锁店有多少家；
（Ⅱ）现从评分类型为A，D的所有商业连锁店中随机抽取两家做分析，求这两家来自同一评分类型的概率．

4．已知数列{a_n}的通项公式为${a_n}=6n+5（n∈{N^*}）$，数列{b_n}是等差数列，且a_n=b_n+b_n+1
（Ⅰ）求数列{a_n}的前n项和；
（Ⅱ）求数列{b_n}的通项公式．