练习册

  • 练习册
  • 试题
    相关习题
     0  235961  235969  235975  235979  235985  235987  235991  235997  235999  236005  236011  236015  236017  236021  236027  236029  236035  236039  236041  236045  236047  236051  236053  236055  236056  236057  236059  236060  236061  236063  236065  236069  236071  236075  236077  236081  236087  236089  236095  236099  236101  236105  236111  236117  236119  236125  236129  236131  236137  236141  236147  236155  266669 

    科目： 来源： 题型：解答题

    17．已知抛物线x2=4y的焦点为F，P为该抛物线上的一个动点．
    （1）当|PF|=2时，求点P的坐标；
    （2）过F且斜率为1的直线与抛物线交与两点AB，若P在弧AB上，求△PAB面积的最大值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．如图，在四棱锥O-ABCD中，底面ABCD是边长为1的菱形，∠ABC=$\frac{π}{4}$，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．
    （1）证明：直线MN∥平面OCD．
    （2）求三棱锥N-CDM的体积．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    15．已知命题p：“$\frac{2{x}^{2}}{m}$+$\frac{{y}^{2}}{m-1}$=1是焦点在x轴上的椭圆的标准方程”，命题q：?x1∈R，8x12-8mx1+7m-6=0．若p∨q为真命题，p∧q为假命题，求实数m的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    14．已知正四面体ABCD，则直线BC与平面ACD所成角的正弦值为$\frac{\sqrt{6}}{3}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    13．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{{\sqrt{2}}}{2}$，左焦点为F（-1，0），过点D（0，2）且斜率为k的直线l交椭圆于A，B两点．
    （1）求椭圆C的标准方程；
    （2）在y轴上，是否存在定点E，使$\overrightarrow{AE}•\overrightarrow{BE}$恒为定值？若存在，求出E点的坐标和这个定值；若不存在，说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    12．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．石景山古城地区2013年2月6日至15日每天的PM2.5监测数据如茎叶图所示．
    （1）小陈在此期间的某天曾经来此地旅游，求当天PM2.5日均监测数据未超标的概率；
    （2）从所给10天的数据中任意抽取三天数据，记ξ表示抽到PM2.5监测数据超标的天数，求ξ的分布列及期望．

    查看答案和解析>>

    科目： 来源： 题型：填空题

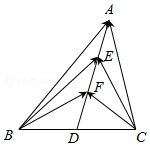    11．如图，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，$\overrightarrow{BA}•\overrightarrow{CA}=8$，$\overrightarrow{BF}•\overrightarrow{CF}=-2$则$\overrightarrow{BE}•\overrightarrow{CE}$的值是$\frac{7}{4}$．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    10．已知{an}为等比数列，若a4+a6=8，则a1a7+2a3a7+a3a9=64．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    9．已知f（x）=x3-3x+3+m（m＞0）．在区间[0，2]上存在三个不同的实数a，b，c，使得以f（a），f（b），f（c）为边长的三角形是直角三角形．则m的取值范围是（　　）
    A．$（3+4\sqrt{2}，+∞）$B．$（2\sqrt{2}-1，+∞）$C．$（0，2\sqrt{2}-1）$D．$（0，3+4\sqrt{2}）$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    8．已知函数f（x）=2sinx-2cosx，$x∈[-\frac{1}{2}，1]$，g（x）=e1-2x．
    （1）求函数f（x）在x=0处的切线方程；
    （2）求证：$x∈[-\frac{1}{2}，1]$时，f（x）≥l（x）恒成立；
    （3）求证：$x∈[-\frac{1}{2}，1]$时，f（x）+g（x）≥0恒成立．

    查看答案和解析>>

    同步练习册答案