科目： 来源： 题型：填空题

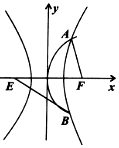5．已知E，F为双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左右焦点，抛物线y²=2px（p＞0）与双曲线有公共的焦点F，且与双曲线交于不同的两点A，B，若$|AF|=\frac{4}{5}|BE|$，则双曲线的离心率为$4±\sqrt{7}$．

科目： 来源： 题型：选择题

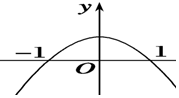4．已知f′（x）是f（x）的导数，且y=xf′（x）的图象如图所示，则下列关于f（x）说法正确的是（　　）

	A．	在（-∞，0）上是增函数		B．	在（-1，1）上是增函数
	C．	在（-1，0）上是增函数		D．	在（1，+∞）上是减函数

科目： 来源： 题型：解答题

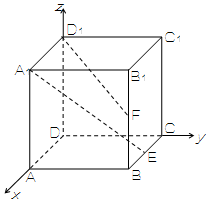3．设点E，F分别是棱长为2的正方体ABCD-A₁B₁C₁D₁的棱BC，BB₁的中点．如图，以D为坐标原点，$\overrightarrow{DA}$，$\overrightarrow{DC}$，$\overrightarrow{D{D_1}}$为x轴、y轴、z轴正方向，建立空间直角坐标系．
（I）求$\overrightarrow{{A_1}E}•\overrightarrow{{D_1}F}$；
（II）若点M，N分别是线段A₁E与线段D₁F上的点，问是否存在直线MN，使得MN⊥平面ABCD？若存在，求点M，N的坐标；若不存在，请说明理由．

科目： 来源： 题型：解答题

2．如图，已知球的半径为3，球内接圆锥的高为h（h＞3），体积为V，
（1）写出以h表示V的函数关系式V（h）；
（2）当h为何值时，V（h）有最大值，并求出该最大值．

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

科目： 来源： 题型：选择题

18．执行如图所示程序框图，输出的k值为（　　）

A．

3

B．

4

C．

5

D．

6

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题