练习册

  • 练习册
  • 试题
    相关习题
     0  236063  236071  236077  236081  236087  236089  236093  236099  236101  236107  236113  236117  236119  236123  236129  236131  236137  236141  236143  236147  236149  236153  236155  236157  236158  236159  236161  236162  236163  236165  236167  236171  236173  236177  236179  236183  236189  236191  236197  236201  236203  236207  236213  236219  236221  236227  236231  236233  236239  236243  236249  236257  266669 

    科目： 来源： 题型：选择题

    2．复数$z=\frac{3+7i}{i}$的实部与虚部分别为（　　）
    A．7，-3B．7，-3iC．-7，3D．-7，3i

    查看答案和解析>>

    科目： 来源： 题型：填空题

    1．已知函数f（x）=$\left\{\begin{array}{l}{（{\frac{1}{2}}）^x}+1，x≥1\\ \frac{3x}{2}，0＜x＜1\end{array}$，若函数g（x）=f（x）-k有两不同的零点，则实数k的取值范围是（1，$\frac{3}{2}$）．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    20．若对任意x∈（0，$\frac{1}{2}$），恒有4x＜logax（a＞0且a≠1），则实数a的取值范围是[$\frac{\sqrt{2}}{2}$，1）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    19．设集合A={x|2≤x＜4}，B={x|3x-7≥8-2x}．
    （1）求集合B，A∪B；   
    （2）求（∁RA）∩B，A∪（∁RB）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．在直角坐标系xOy中，曲线C1的参数方程为$\left\{\begin{array}{l}x=\sqrt{3}+tcosα\\ y=2+tsinα\end{array}\right.（t$是参数），以原点O为极点，x轴正半轴为极轴建立极坐标系，C2曲线的极坐标方程为ρ2=4$\sqrt{2}$ρsin（$θ+\frac{π}{4}$）-4．
    （1）求曲线C2的直角坐标方程，并指出其表示何种曲线；
    （2）若曲线C1与曲线C2交于A，B两点，求|AB|的最大值和最小值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    17．已知函数f（x）=lnx-x2+x．
    （1）求函数f（x）的单调区间；
    （2）证明当a≥2时，关于x的不等式$f（x）＜（{\frac{a}{2}-1}）{x^2}+ax-1$恒成立；
    （3）若正实数x1，x2满足$f（{x_1}）+f（{x_2}）+2（{x_1^2+x_2^2}）+{x_1}{x_2}=0$，证明${x_1}+{x_2}≥\frac{{\sqrt{5}-1}}{2}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．已知点C的坐标为（1，0），A，B是抛物线y2=x上不同于原点O的相异的两个动点，且$\overrightarrow{OA}•\overrightarrow{OB}=0$．
    （1）求证：点A，C，B共线；
    （2）若$\overrightarrow{AQ}=λ\overrightarrow{QB}（{λ∈R}）$，当$\overrightarrow{OQ}•\overrightarrow{AB}=0$时，求动点Q的轨迹方程．

    查看答案和解析>>

    科目： 来源： 题型：解答题

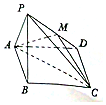    15．如图，已知四棱锥P-ABCD中，底面ABCD为菱形，且∠DAB=60°，△PAB是边长为a的正三角形，且平面PAB⊥平面ABCD，已知点M是PD的中点．
    （1）证明：PB∥平面AMC；
    （2）求三棱锥P-AMC的体积．

    查看答案和解析>>

    科目： 来源： 题型：解答题

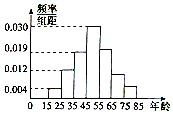    14．某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况，随机调查了100位到购物中心购物的顾客年龄，并整理后画出频率分布直方图如图所示，年龄落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1．
    （1）求顾客年龄值落在区间[75，85]内的频率；
    （2）拟利用分层抽样从年龄在[55，65），[65，75）的顾客中选取6人召开一个座谈会，现从这6人中选出2人，求这两人在不同年龄组的概率．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    13．设数列{an}的前n项和为Sn，已知${a_1}=1，{a_{n+1}}=3{S_n}+1，n∈{N^*}$．
    （1）求a2，a3的值；
    （2）求数列{an}的通项公式．

    查看答案和解析>>

    同步练习册答案