练习册

  • 练习册
  • 试题
    相关习题
     0  236083  236091  236097  236101  236107  236109  236113  236119  236121  236127  236133  236137  236139  236143  236149  236151  236157  236161  236163  236167  236169  236173  236175  236177  236178  236179  236181  236182  236183  236185  236187  236191  236193  236197  236199  236203  236209  236211  236217  236221  236223  236227  236233  236239  236241  236247  236251  236253  236259  236263  236269  236277  266669 

    科目： 来源： 题型：选择题

    2．若集合${A}=\{x|\frac{x+5}{x-2}≤0\}$，B={x||x|＜3}，则集合 A∪B为（　　）
    A．{x|-5＜x＜3}B．{x|-3＜x＜2}C．{x|-5≤x＜3}D．{x|-3＜x≤2}

    查看答案和解析>>

    科目： 来源： 题型：解答题

    1．（1）已知函数f（x）=2x+$\frac{1}{x}$（x＞0），证明函数f（x）在（0，$\frac{\sqrt{2}}{2}$）上单调递减，并写出函数f（x）的单调递增区间；
    （2）记函数g（x）=a|x|+2ax（a＞1）
    ①若a=4，解关于x的方程g（x）=3；
    ②若x∈[-1，+∞），求函数g（x）的值域．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    20．已知函数f（x）=m（sinx+cosx）-4sinxcosx，x∈[0，$\frac{π}{2}$]，m∈R．
    （1）设t=sinx+cosx，x∈[0，$\frac{π}{2}$]，将f（x）表示为关于t的函数关系式g（t），并求出t的取值范围；
    （2）若关于x的不等式f（x）≥0对所有的x∈[0，$\frac{π}{2}$]恒成立，求实数m的取值范围；
    （3）若关于x的方程f（x）-2m+4=0在[0，$\frac{π}{2}$]上有实数根，求实数m的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    19．如图，经过村庄A有两条互相垂直的笔直公路AB和AC，根据规划拟在两条公路围成的直角区域内建一工厂P，为了仓库存储和运输方便，在两条公路上分别建两个仓库M，N（异于村庄A，将工厂P及仓库M，N近似看成点，且M，N分别在射线AB，AC上），要求MN=2，PN=1（单位：km），PN⊥MN．
    （1）设∠AMN=θ，将工厂与村庄的距离PA表示为θ的函数，记为l（θ），并写出函数l（θ）的定义域；
    （2）当θ为何值时，l（θ）有最大值？并求出该最大值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．若|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=m，|$\overrightarrow{a}$+$\overrightarrow{b}$|=2．
    （1）若|$\overrightarrow{a}$+2$\overrightarrow{b}$|=3，求实数m的值；
    （2）若$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为$\frac{2π}{3}$，求实数m的值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

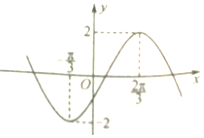    17．已知函数f（x）=Asin（ωx-$\frac{π}{6}$）（其中A，ω为常数，且A＞0，ω＞0）的部分图象如图所示．
    （1）求函数f（x）的解析式；
    （2）若f（α+$\frac{π}{6}$）=$\frac{2\sqrt{5}}{5}$，f（β+$\frac{2π}{3}$）=$\frac{3\sqrt{10}}{5}$，且α，β∈（0，$\frac{π}{2}$），求α+β的值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．已知集合A={x|f（x）=lg（x-1）+$\sqrt{2-x}$}，集合B={y|y=2x+a，x≤0}．
    （1）若a=$\frac{3}{2}$，求A∪B；
    （2）若A∩B=∅，求实数a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    15．如图，在△ABC中，已知AB=2，AC=3，∠BAC=60°，点D，E分别在边AB，AC上，且$\overrightarrow{AB}$=2$\overrightarrow{AD}$，$\overrightarrow{AC}$=3$\overrightarrow{AE}$，点F位线段DE上的动点，则$\overrightarrow{BF}$•$\overrightarrow{CF}$的取值范围是[-$\frac{1}{16}$，$\frac{1}{2}$]．（　　）

    查看答案和解析>>

    科目： 来源： 题型：填空题

    14．已知函数f（x）=cosx（x∈[0，2π]）与函数g（x）=tanx的图象交于M，N两点，则|$\overrightarrow{OM}$+$\overrightarrow{ON}$|=π．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    13．在平面直角坐标系xOy中，点P（1，4）是角α终边上一点，将射线OP绕坐标原点O逆时针方向旋转θ（0＜θ＜π）角后到达角$\frac{3}{4}$π的终边，则tanθ=$\frac{5}{3}$．

    查看答案和解析>>

    同步练习册答案