练习册

  • 练习册
  • 试题
    相关习题
     0  236314  236322  236328  236332  236338  236340  236344  236350  236352  236358  236364  236368  236370  236374  236380  236382  236388  236392  236394  236398  236400  236404  236406  236408  236409  236410  236412  236413  236414  236416  236418  236422  236424  236428  236430  236434  236440  236442  236448  236452  236454  236458  236464  236470  236472  236478  236482  236484  236490  236494  236500  236508  266669 

    科目： 来源： 题型：选择题

    15．湖心有四座小岛，其中任何三座都不在一条直线上．拟在它们之间修建3座桥，以便从其中任何一座小岛出发皆可通过这三座桥到达其它小岛．则不同的修桥方案有（　　）
    A．4种B．16种C．20种D．24种

    查看答案和解析>>

    科目： 来源： 题型：选择题

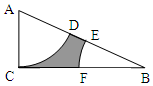    14．如图，在Rt△ACB中，∠ACB=90°，BC=2AC，分别以A、B为圆心，AC的长为半径作扇形ACD和扇形BEF，D、E在AB上，F在BC上．在△ACB中任取一点，这一点恰好在图中阴影部分的概率是（　　）
    A．$\frac{π}{8}$B．1-$\frac{π}{8}$C．$\frac{π}{4}$D．1-$\frac{π}{4}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    13．代数式$（\sqrt{x}+2）{（\frac{1}{{\sqrt{x}}}-1）^5}$的展开式中，常数项是（　　）
    A．-7B．-3C．3D．7

    查看答案和解析>>

    科目： 来源： 题型：选择题

    12．两个实习生每人加工一个零件，加工为一等品的概率分别为$\frac{2}{3}$和$\frac{1}{2}$，两个零件是否加工为一等品相互独立，则这两个零件中至少有一个加工为一等品的概率为（　　）
    A．$\frac{1}{6}$B．$\frac{5}{6}$C．$\frac{1}{3}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    11．设随机变量ξ～N（3，4），若P（ξ＜2a-3）=P（ξ＞a+2），则实数a等于（　　）
    A．$\frac{7}{3}$B．$\frac{5}{3}$C．5D．3

    查看答案和解析>>

    科目： 来源： 题型：选择题

    10．某工厂生产A、B、C三种不同型号的产品，产品数量之比依次为2：3：5，现用分层抽样方法抽出一个容量为n的样本，样本中B种型号产品比A种型号产品多8件．那么此样本的容量n=（　　）
    A．80B．120C．160D．60

    查看答案和解析>>

    科目： 来源： 题型：解答题

    9．已知数列{an}，{bn}满足bn=an+1-an（n=1，2，3，…）．
    （1）若bn=10-n，求a16-a5的值；
    （2）若${b_n}={（-1）^n}（{2^n}+{2^{33-n}}）$且a1=1，则数列{a2n+1}中第几项最小？请说明理由；
    （3）若cn=an+2an+1（n=1，2，3，…），求证：“数列{an}为等差数列”的充分必要条件是“数列{cn}为等差数列且bn≤bn+1（n=1，2，3，…）”．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    8．已知集合M是满足下列性质的函数f（x）的全体：在定义域内存在实数t，使得f（t+2）=f（t）+f（2）．
    （1）判断f（x）=3x+2是否属于集合M，并说明理由；
    （2）若$f（x）=lg\frac{a}{{{x^2}+2}}$属于集合M，求实数a的取值范围；
    （3）若f（x）=2x+bx2，求证：对任意实数b，都有f（x）∈M．

    查看答案和解析>>

    科目： 来源： 题型：解答题

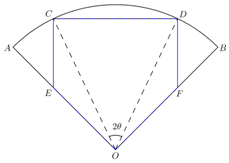    7．现有半径为R、圆心角（∠AOB）为90°的扇形材料，要裁剪出一个五边形工件OECDF，如图所示．其中E，F分别在OA，OB上，C，D在$\widehat{AB}$上，且OE=OF，EC=FD，∠ECD=∠CDF=90°．记∠COD=2θ，五边形OECDF的面积为S．
    （1）试求S关于θ的函数关系式；
    （2）求S的最大值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    6．已知双曲线C以F1（-2，0）、F2（2，0）为焦点，且过点P（7，12）．
    （1）求双曲线C与其渐近线的方程；
    （2）若斜率为1的直线l与双曲线C相交于A，B两点，且$\overrightarrow{OA}⊥\overrightarrow{OB}$（O为坐标原点）．求直线l的方程．

    查看答案和解析>>

    同步练习册答案