6．函数$f（x）=-x+\frac{1}{x}$在$[{-2，-\frac{1}{3}}]$上的最大值是（　　）

A．

$\frac{3}{2}$

B．

$-\frac{8}{3}$

C．

-2

D．

2

5．复数（1+i）z=1-i（其中i为虚数单位），则z²等于（　　）

A．

1

B．

-1

C．

i

D．

-i

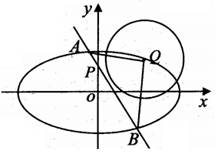4．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，圆Q：x²+y²-4x-2y+3=0的圆心Q在椭圆C上，点P（0，1）到椭圆C的右焦点的距离为2．
（1）求椭圆C的方程；
（2）过点P作直线l交椭圆C于A，B两点，若S_△AQB=tan∠AQB，求直线l的方程．

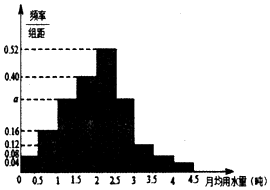3．水是地球上宝贵的资源，由于价格比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费．某市政府为了提倡低碳环保的生活理念鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），[1，1.5），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．
（1）若全市居民中月均用水量不低于3吨的人数为3.6万，试估计全市有多少居民？并说明理由；
（2）若该市政府拟采取分层抽样的方法在用水量吨数为[1，1.5）和[1.5，2）之间选取7户居民作为议价水费价格听证会的代表，并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖，设X为用水量吨数在[1，1.5）中的获奖的家庭数，Y为用水量吨数在[1.5，2）中的获奖家庭数，记随机变量Z=|X-Y|，求Z的分布列和数学期望．

2．已知公比不为1的等比数列{a_n}的前5项积为243，且2a₃为3a₂和a₄的等差中项．
（1）求数列{a_n}的通项公式a_n；
（2）若数列{b_n}满足b_n=b_n-1•log₃a_n+2（n≥2且n∈N*），且b₁=1，求数列$\left\{{\frac{（n-1）!}{{{b_{n+1}}}}}\right\}$的前n项和S_n．

1．已知函数$f（x）=4sin（2x+\frac{π}{6}）$（$0≤x≤\frac{91π}{6}$），若函数F（x）=f（x）-3的所有零点依次记为x₁，x₂，x₃，…，x_n，且x₁＜x₂＜x₃＜…＜x_n，则x₁+2x₂+2x₃+…+2x_n-1+x_n=445π．

20．在边长为1的正方形ABCD中，$2\overrightarrow{AE}=\overrightarrow{EB}$，BC的中点为F，$\overrightarrow{EF}=2\overrightarrow{FG}$，则$\overrightarrow{EG}•\overrightarrow{BD}$=$-\frac{1}{4}$．

19．已知△ABC外接圆半径是2，$BC=2\sqrt{3}$，则△ABC的面积最大值为$3\sqrt{3}$．

18．已知x，y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ 5x-3y-12≥0\\ y≤3\end{array}\right.$当目标函数z=ax+by（a＞0，b＞0）在该约束条件下取得最小值1时，则$\frac{1}{3a}+\frac{2}{b}$的最小值为（　　）

A．

$4+2\sqrt{2}$

B．

$4\sqrt{2}$

C．

$3+2\sqrt{2}$

D．

$3+\sqrt{2}$

17．已知$sin（α-\frac{π}{12}）=\frac{1}{3}$，则$cos（α+\frac{17π}{12}）$的值等于（　　）

A．

$\frac{1}{3}$

B．

$\frac{{2\sqrt{2}}}{3}$

C．

$-\frac{1}{3}$

D．

$-\frac{{2\sqrt{2}}}{3}$