19．命题P：“方程x²+mx+1=0有两个相异负根”，命题Q：“方程4x²+4（m-2）x+1=0无实根”，如果“P或Q”为真，“P且Q”为假，试求实数m的取值范围．

18．已知圆O：x²+y²=2，直线l过两点A（1，-$\frac{3}{2}$），B（4，0）
（1）求直线l的方程；
（2）若P是直线l上的动点，过P作圆O的两条切线PC，PD，切点为C，D，求证：直线CD过定点，并求出定点坐标．

17．巴西世界杯足球赛正在如火如荼进行．某人为了了解我校学生“通过电视收看世界杯”是否与性别有关，从全校学生中随机抽取30名学生进行了问卷调查，得到了如下列联表：

	男生	女生	合计
收看	10
不收看		8
合计			30

已知在这30名同学中随机抽取1人，抽到“通过电视收看世界杯”的学生的概率是$\frac{8}{15}$．
（I）请将上面的列联表补充完整，并据此资料分析在犯错误概率不超过0.01的前提下“通过电视收看世界杯”与性别是否有关？
（II）若从这30名同学中的男同学中随机抽取2人参加一活动，记“通过电视收看世界杯”的人数为X，求X的分布列和均值．
（参考公式：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（c+a）（b+d）}$，n=a+b+c+d）

P（K2＞k0）	0.100	0.050	0.010
k0	2.706	3.841	6.635

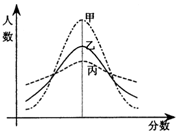16．某次市教学质量检测，甲、乙、丙三科考试成绩的直方图如图所示（由于人数众多，成绩分布的直方图可视为正态分布），则由图中曲线可得下列说法中正确的一个是（　　）

	A．	甲、乙、丙的总体的平均数不相同		B．	乙科总体的标准差及平均数都居中
	C．	丙科总体的平均数最小		D．	甲科总体的标准差最小

15．如表提供了某厂节能降耗技术改造后在生产A产品过程中纪录的产量x（吨）与相应的生产能耗y（吨）的几组对应数据：

x	3	4	5	6
y	2.5	n	4	4.5

根据上表提供的数据，求得y关于x的线性回归方程为$\widehat{y}$=0.7x+0.35，那么表中n的值为（　　）注（$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$，$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$）

A．

3

B．

3.15

C．

3.5

D．

4.5

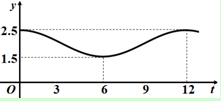14．某企业一天中不同时刻的用电量y（万千瓦时）关于时间t（小时，0≤t≤24）的函数y=f（t）近似满足f（t）=Asin（ωt+φ）+B，（A＞0，ω＞0，0＜φ＜π）．如图是函数y=f（t）的部分图象（t=0对应凌晨0点）．
（Ⅰ）根据图象，求A，ω，φ，B的值；
（Ⅱ）由于当地冬季雾霾严重，从环保的角度，既要控制火力发电厂的排放量，电力供应有限；又要控制企业的排放量，于是需要对各企业实行分时拉闸限电措施．已知该企业某日前半日能分配到的供电量g（t）（万千瓦时）与时间t（小时）的关系可用线性函数模型g（t）=-2t+25（0≤t≤12）模拟．当供电量小于该企业的用电量时，企业就必须停产．初步预计停产时间在中午11点到12点间，为保证该企业既可提前准备应对停产，又可尽量减少停产时间，请从这个初步预计的时间段开始，用二分法帮其估算出精确到15分钟的停产时间段．

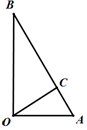13．根据平面向量基本定理，若$\overrightarrow{e_1}，\overrightarrow{e_2}$为一组基底，同一平面的向量$\overrightarrow a$可以被唯一确定地表示为$\overrightarrow a=x\overrightarrow{e_1}+y\overrightarrow{e_2}$，则向量$\overrightarrow a$与有序实数对（x，y）一一对应，称（x，y）为向量$\overrightarrow a$在基底$\overrightarrow{e_1}，\overrightarrow{e_2}$下的坐标；特别地，若$\overrightarrow{e_1}，\overrightarrow{e_2}$分别为x，y轴正方向的单位向量$\overrightarrow i，\overrightarrow j$，则称（x，y）为向量$\overrightarrow a$的直角坐标．
（I）据此证明向量加法的直角坐标公式：若$\overrightarrow a=（{x_1}，{y_1}），\overrightarrow b=（{x_2}，{y_2}）$，则$\overrightarrow a+\overrightarrow b=（{x_1}+{x_2}，{y_1}+{y_2}）$；
（II）如图，直角△OAB中，$∠AOB={90°}，|\overrightarrow{OA}|=1，|\overrightarrow{OB}|=\sqrt{3}$，C点在AB上，且$\overrightarrow{OC}⊥\overrightarrow{AB}$，求向量$\overrightarrow{OC}$在基底$\overrightarrow{OA}，\overrightarrow{OB}$下的坐标．

12．已知函数$f（x）=\frac{3-a}{{{a^x}+1}}+asinx$，那么下列命题正确的是（　　）

	A．	若a=0，则y=f（x）与y=3是同一函数
	B．	若0＜a≤1，则$f（-\frac{π}{2}）＜f（2-{log_3}2）＜f[{（\frac{1}{3}）^{{{log}_3}\frac{2}{3}}}]＜f（{log_3}5）＜f（\frac{π}{2}）$
	C．	若a=2，则对任意使得f（m）=0的实数m，都有f（-m）=1
	D．	若a＞3，则f（cos2）＜f（cos3）

11．已知圆C：x²+y²-4x+3=0，
（1）求过M（3，2）点的圆的切线方程；
（2）直线l：2mx+2y-1-3m=0被圆C截得的弦长最短时，求直线l的方程；
（3）过原点的直线m与圆C交于不同的两点A、B，线段AB的中点P的轨迹为C₁，直线$y=k（x-\frac{5}{2}）$与曲线C₁只有一个交点，求k的取值范围．

10．下列说法正确的是（　　）

	A．	命题“若x2＞1，则x＞1”的否命题为“若x2＞1，则x≤1”
	B．	命题“若$?{x_0}∈R，{x_0}^2＞1$”的否定是“?x∈R，x2＜1”
	C．	命题“若x=y，则cosx=cosy”的逆否命题为假命题
	D．	命题“若x=y，则cosx=cosy”的逆命题为假命题