19.二手车经销商小王对其所经营的A型号二手汽车的使用年数x与销售价格y(单位:万元/辆)进行整理,得到如下数据:
| 使用年数x | 2 | 3 | 4 | 5 | 6 | 7 |
| 售价y | 20 | 12 | 8 | 6.4 | 4.4 | 3 |
| z=lny | 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |
下面是z关于x的折线图:
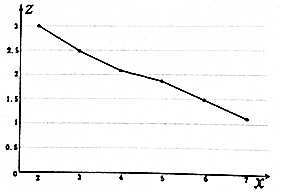
(1)由折线图可以看出,可以用线性回归模型拟合z与x的关系,请用相关数加以说明;
(2)求y关于x的回归方程并预测某辆A型号二手车当使用年数为9年时售价约为多少?($\widehat{b}$、$\widehat{a}$小数点后保留两位有效数字).
(3)基于成本的考虑,该型号二手车的售价不得低于7118元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
参考公式:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中斜率和截距的最小二乘估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$.
参考数据:
$\sum_{i=1}^{6}{x}_{i}{y}_{i}$=187.4,$\sum_{i=1}^{6}{x}_{i}{z}_{i}$=47.64,$\sum_{i=1}^{6}{{x}_{i}}^{2}$=139,$\sqrt{\sum_{i=1}^{6}({x}_{i}-\overline{x})^{2}}$=4.18,$\sqrt{\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}}$=13.96,
$\sqrt{\sum_{i=1}^{6}({z}_{i}-\overline{z})^{2}}$=1.53,ln1.46≈0.38,ln0.7118≈-0.34.

