10．在三棱锥P-ABC中，PA，PB，PC两两互相垂直，且AB=4，AC=5，则BC的取值范围是（3，$\sqrt{41}$）．

9．我国古代数学家祖暅是著名数学家祖冲之之子，祖暅原理叙述道：“夫叠棋成立积，缘幂势既同，则积不容异．”意思是：夹在两个平行平面之间的两个几何体被平行于这两个平行平面的任意平面所截，如果截得的两个截面面积总相等，那么这两个几何体的体积相等．其最著名之处是解决了“牟合方盖”中的体积问题，其核心过程为：如下图正方体ABCD-A₁B₁C₁D₁，求图中四分之一圆柱体BB₁C₁-AA₁D₁和四分之一圆柱体AA₁B₁-DD₁C₁公共部分的体积V，若图中正方体的棱长为2，则V=（　　）  
（在高度h处的截面：用平行于正方体上下底面的平面去截，记截得两圆柱体公共部分所得面积为S₁，截得正方体所得面积为S₂，截得锥体所得面积为S₃，${S_1}={R^2}-{h^2}$，${S_2}={R^2}$⇒S₂-S₁=S₃）

A．

$\frac{16}{3}$

B．

$\frac{8}{3}$

C．

8

D．

$\frac{8π}{3}$

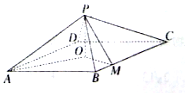8．如图，四棱锥P-ABCD中，底面是以O为中心的菱形，PO⊥底面$ABCD，AB=2，∠BAD=\frac{π}{3}，M$为BC上一点，且$BM=\frac{1}{2}$．
（1）证明：BC⊥平面POM；
（2）若MP⊥AP，求四棱锥P-ABCD的体积．

7．如图，在棱台ABC-FED中，△DEF与△ABC分别是棱长为1与2的正三角形，平面ABC⊥平面BCDE，四边形BCDE为直角梯形，BC⊥CD，CD=1，点G为△ABC的重心，N为AB中点，$\overrightarrow{AM}$=λ$\overrightarrow{AF}$（λ∈R，λ＞0），
（1）当$λ=\frac{2}{3}$时，求证：GM∥平面DFN；
（2）若直线MN与CD所成角为$\frac{π}{3}$，试求二面角M-BC-D的余弦值．

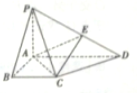6．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，BC∥AD，∠ABC=90°，且PA=AB=BC=$\frac{1}{2}$AD=1，点E在棱PD上（点E异于端点），且$\overrightarrow{PE}=λ\overrightarrow{PD}$．
（1）当$λ=\frac{2}{3}$时，求异面直线PC与AE所成角的余弦值；
（2）若二面角P-AC-E的余弦值为$\frac{\sqrt{3}}{3}$，求λ的值．

5．如图，在三棱柱ABC-A₁B₁C₁中，AB⊥平面BCC₁B₁，$∠BC{C_1}=\frac{π}{3}，AB=B{B_1}=2，BC=1，D$为CC₁的中点．
（1）求证：DB₁⊥平面ABD；
（2）求点A₁到平面ADB₁的距离．

4．已知函数f（x）=|2x+1|+|x-3|-7．
（1）在图中画出y=f（x）的图象；
（2）求不等式|f（x）|＞1的解集．

3．在平面直角坐标系xOy中，抛物线C的方程为x²=4y+4．
（1）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；
（2）直线l的参数方程是$\left\{{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}}\right.$（t为参数），l与C交于A，B两点，|AB|=8，求l的斜率．

2．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左焦点F₁（-1，0），C的离心率为e，b是3e和a的等比中项．
（1）求曲线C的方程；
（2）倾斜角为α的直线过原点O且与C交于A，B两点，倾斜角为β的直线过F₁且与C交于D，E两点，若α+β=π，求$\frac{{{{|{AB}|}^2}}}{{|{DE}|}}$的值．

1．已知函数f（x）=axe^x-（a-1）（x+1）²（其中a∈R，e为自然对数的底数，e=2.718128…）．
（1）当a=-1时，求f（x）的单调区间；
（2）若f（x）仅有一个极值点，求a的取值范围．