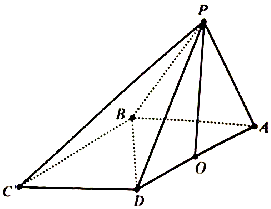10．在四棱锥P-ABCD中，$∠DBA=\frac{π}{2}$，$AB\underline{\underline∥}CD$，△PAB和△PBD都是边长为2的等边三角形，设P在底面ABCD的射影为O．
（1）求证：O是AD中点；
（2）证明：BC⊥PB；
（3）求二面角A-PB-C的余弦值．

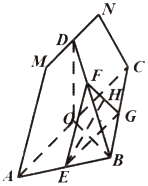9．如图所示，四边形AMNC为等腰梯形，△ABC为直角三角形，平面AMNC与平面ABC垂直，AB=BC，AM=CN，点O、D、E分别是AC、MN、AB的中点．过点E作平行于平面AMNC的截面分别交BD、BC于点F、G，H是FG的中点．
（Ⅰ）证明：OB⊥EH；
（Ⅱ）若直线BH与平面EFG所成的角的正弦值为$\frac{{\sqrt{6}}}{3}$，求二面角D-AC-H的余弦值．

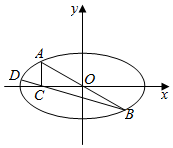8．已知焦距为2的椭圆W：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为A₁，A₂，上、下顶点分别为B₁，B₂，点M（x₀，y₀）为椭圆W上不在坐标轴上的任意一点，且四条直线MA₁，MA₂，MB₁，MB₂的斜率之积为$\frac{1}{4}$．
（1）求椭圆W的标准方程；
（2）如图所示，点A，D是椭圆W上两点，点A与点B关于原点对称，AD⊥AB，点C在x轴上，且AC与x轴垂直，求证：B，C，D三点共线．

7．5位同学站成一排照相，其中甲与乙必须相邻，且甲不能站在两端的排法总数是（　　）

A．

40

B．

36

C．

32

D．

24

6．某闯关游戏规则是：先后掷两枚骰子，将此试验重复n轮，第n轮的点数分别记为x_n，y_n，如果点数满足x_n＜$\frac{6{y}_{n}}{{y}_{n}+6}$，则认为第n轮闯关成功，否则进行下一轮投掷，直到闯关成功，游戏结束．
（I）求第一轮闯关成功的概率；
（Ⅱ）如果第i轮闯关成功所获的奖金数f（i）=10000×$\frac{1}{{2}^{i}}$（单位：元），求某人闯关获得奖金不超过1250元的概率；
（Ⅲ）如果游戏只进行到第四轮，第四轮后不论游戏成功与否，都终止游戏，记进行的轮数为随机变量X，求x的分布列和数学期望．

5．点M（3，2）到拋物线C：y=ax²（a＞0）准线的距离为4，F为拋物线的焦点，点N（l，l），当点P在直线l：x-y=2上运动时，$\frac{|PN|-1}{|PF|}$的最小值为（　　）

A．

$\frac{3-2\sqrt{2}}{8}$

B．

$\frac{2-\sqrt{2}}{4}$

C．

$\frac{5-2\sqrt{2}}{8}$

D．

$\frac{5-2\sqrt{2}}{4}$

4．已知f（x）=|x+a|，g（x）=|x+3|-x，记关于x的不等式f（x）＜g（x）的解集为M．
（1）若a-3∈M，求实数a的取值范围；
（2）若[-1，1]⊆M，求实数a的取值范围．

3．已成椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右顶点分别为A₁、A₂，上下顶点分别为B₂/B₁，左右焦点分别为F₁、F₂，其中长轴长为4，且圆O：x²+y²=$\frac{12}{7}$为菱形A₁B₁A₂B₂的内切圆．
（1）求椭圆C的方程；
（2）点N（n，0）为x轴正半轴上一点，过点N作椭圆C的切线l，记右焦点F₂在l上的射影为H，若△F₁HN的面积不小于$\frac{3}{16}$n²，求n的取值范围．

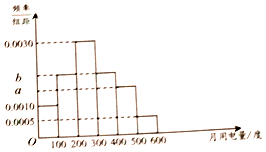2．某市为了鼓励市民节约用电，实行“阶梯式”电价，将该市每户居民的月用电量划分为三档，月用电量不超过200度的部分按0.5元/度收费，超过200度但不超过400度的部分按0.8元/度收费，超过400度的部分按1.0元/度收费．
（1）求某户居民用电费用y（单位：元）关于月用电量x（单位：度）的函数解析式；
（2）为了了解居民的用电情况，通过抽样，获得了今年1月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图，若这100户居民中，今年1月份用电费用不超过260元的点80%，求a，b的值；
（3）在满足（2）的条件下，若以这100户居民用电量的频率代替该月全市居民用户用电量的概率，且同组中的数据用该组区间的中点值代替，记Y为该居民用户1月份的用电费用，求Y的分布列和数学期望．

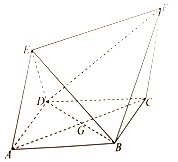1．如图，四边形ABCD为菱形，四边形ACEF为平行四边形，设BD与AC相交于点G，AB=BD=2，AE=$\sqrt{3}$，∠EAD=∠EAB．
（1）证明：平面ACEF⊥平面ABCD；
（2）若AE与平面ABCD所成角为60°，求二面角B-EF-D的余弦值．