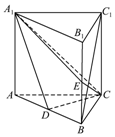20．如图，直三棱柱ABC-A₁B₁C₁中，D，E分别是AB，BB₁的中点，AA₁=AC=CB=2，AB=2$\sqrt{2}$．
（Ⅰ）证明：BC₁∥平面A₁CD；
（Ⅱ）求锐二面角D-A₁C-E的余弦值．

19．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右顶点分别为A₁，A₂，左、右焦点分别为F₁，F₂，离心率为$\frac{1}{2}$，点B（4，0），F₂为线段A₁B的中点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过点B且斜率不为0的直线l与椭圆C交于M，N两点，已知直线A₁M与A₂N相交于点G，求证：以点G为圆心，GF₂的长为半径的圆总与x轴相切．

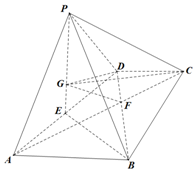18．如图，四棱锥P-ABCD中，平面PAD⊥平面ABCD，底面ABCD为梯形，AB∥CD，AB=2DC=2$\sqrt{3}$，AC∩BD=F．且△PAD与△ABD均为正三角形，E为AD的中点，G为△PAD重心．
（Ⅰ）求证：GF∥平面PDC；
（Ⅱ）求三棱锥G-PCD的体积．

17．如图（1），在四棱锥P-ABCD中，底面为正方形，PC与底面ABCD垂直，图（2）为该四棱锥的正视图和侧视图，它们是腰长为6cm的全等的等腰直角三角形．

（1）根据图所给的正视图、侧视图，画出相应的俯视图，并求出该俯视图的面积；
（2）在四棱锥P-ABCD中，求PA的长．

16．若函数f（x）满足$f（{x-1}）=\frac{1}{f（x）-1}$，当x∈[-1，0]时，f（x）=x，若在区间[-1，1]上，g（x）=f（x）-mx+m有两个零点，则实数m的取值范围为（0，$\frac{1}{2}$]．

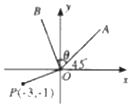15．如图，已知点P（-3，-1），OA为第一象限的角平分线，将OA沿逆时针旋转θ角到OB，若$\overrightarrow{OP}•\overrightarrow{OB}=0$，则tanθ的值为（　　）

A．

2

B．

3

C．

-2

D．

-3

14．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，其左、右焦点分别为F₁，F₂，点P是坐标平面内一点，且$|{\overrightarrow{OP}}|=\frac{{\sqrt{7}}}{2}，\overrightarrow{P{F_1}}•{\overrightarrow{PF}_2}=\frac{3}{4}$，其中O为坐标原点．
（1）求椭圆C的方程；
（2）过点$S（{0，\frac{1}{3}}）$，且斜率为k的直线l交椭圆于A，B两点，在y轴上是否存在定点M，使得以AB为直径的圆恒过这个定点？若存在，求出点M的坐标；若不存在，请说明理由．

13．已知O为坐标原点，圆M：（x+1）²+y²=16，定点F（1，0），点N是圆M上一动点，线段NF的垂直平分线交圆M的半径MN于点Q，点Q的轨迹为E．
（1）求曲线E的方程；
（2）已知点P是曲线E上但不在坐标轴上的任意一点，曲线E与y轴的交点分别为B₁、B₂，直线B₁P和B₂P分别与x轴相交于C、D两点，请问线段长之积|OC|•|OD|是否为定值？如果是请求出定值，如果不是请说明理由；
（3）在（2）的条件下，若点C坐标为（-1，0），过点C的直线l与E相交于A、B两点，求△ABD面积的最大值．

12．如图，在三棱柱ABC-A₁B₁C₁中，AB⊥平面BB₁C₁C，且四边形BB₁C₁C是菱形，∠BCC₁=60°．
（1）求证：AC₁⊥B₁C；
（2）若AC⊥AB₁，三棱锥A-BB₁C的体积为$\frac{\sqrt{6}}{3}$，求△ABC的面积．

11．如图所示，在三棱锥P-ABC中，已知PC⊥平面ABC，点C在平面PBA内的射影D在直线PB上．
（1）求证：AB⊥平面PBC；
（2）设AB=BC，直线PA与平面ABC所成的角为45°，求二面角C-PA-B的余弦值．