10．已知函数$f=\frac{1}{e^x}+x+{m^2}.x∈R$．的单调区间,(Ⅱ)若存在x∈[0.2].使得f＜0成立.求m的取值范围,(Ⅲ)设x1.x2(x1≠x2)是函数f(x)的两个零——青夏教育精英家教网—

相关习题

0 237080 237088 237094 237098 237104 237106 237110 237116 237118 237124 237130 237134 237136 237140 237146 237148 237154 237158 237160 237164 237166 237170 237172 237174 237175 237176 237178 237179 237180 237182 237184 237188 237190 237194 237196 237200 237206 237208 237214 237218 237220 237224 237230 237236 237238 237244 237248 237250 237256 237260 237266 237274 266669

科目： 来源： 题型：解答题

10．已知函数$f（x）={e^x}-x+2m+3，g（x）=\frac{1}{e^x}+x+{m^2}，x∈R$．
（I）求函数f（x）的单调区间；
（Ⅱ）若存在x∈[0，2]，使得f（x）-g（x）＜0成立，求m的取值范围；
（Ⅲ）设x₁、x₂（x₁≠x₂）是函数f（x）的两个零点，求证：x₁+x₂＜0．

查看答案和解析>>

科目： 来源： 题型：解答题

9．已知数列{a_n}的前n项和为S_n，且S_n+2=2a_n•等差数列{b_n}的前n项和为T_n，且T₂=S₂=b_3•
（I）求数列{b_n}的通项公式；
（Ⅱ）令${c_n}={（-1）^n}\frac{{4{T_n}-1}}{b_n^2-1}$，求数列{c_n}的前2n项和R_2n．

查看答案和解析>>

科目： 来源： 题型：解答题

8．一厂家生产A、B、C三类空气净化器，每类净化器均有经典版和至尊版两种型号，某月的产量如表（单位：台）：

	空气净化器A	空气净化器B	空气净化器C
经典版	100	150	400
至尊版	300	450	600

（I）在C类空气净化器中，用分层抽样的方法抽取一个容量为5的样本．将该样本看成一个总体，从中任取2辆，求至少有1台经典版空气净化器的概率；
（Ⅱ）用随机抽样的方法从B类空气净化器中抽取8台，经检测它们的得分如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2．把这8台空气净化器的得分看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0.5的概率．

查看答案和解析>>

科目： 来源： 题型：解答题

7．已知f（x）=$\overrightarrow a•\overrightarrow b$，其中$\overrightarrow a=（2cosx，-\sqrt{3}sin2x），\overrightarrow b=（cosx，1），x∈R$．
（I）求f（x）在区间[-π，π]上的单调递增区间；
（Ⅱ）在△ABC中，角A、B、C所对的边分别为a、b、c，f（A）=-1，a=$\frac{{\sqrt{7}}}{2}$，且向量$\overrightarrow m=（sinB，-3）与\overrightarrow n=（2，sinC）$垂直，求边长b和c的值．

查看答案和解析>>

科目： 来源： 题型：填空题

6．

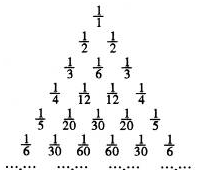德国数学家莱布尼兹发现了右面的单位分数三角形，单位分数是分子为1，分母为正整数的分数称为莱布尼兹三角形：根据前6行的规律，写出第7行的第3个数是$\frac{1}{105}$．