18．在平面直角坐标系xOy中，曲线C的参数方程为$\left\{\begin{array}{l}{x=a+acosβ}\\{y=asinβ}\end{array}\right.$（a＞0，β为参数），以O为极点，x轴的正半轴为极轴，建立极坐标系，直线l的极坐标方程ρcos（θ-$\frac{π}{3}$）=$\frac{3}{2}$．
（Ⅰ）若曲线C与l只有一个公共点，求a的值；
（Ⅱ）A，B为曲线C上的两点，且∠AOB=$\frac{π}{3}$，求△OAB的面积最大值．

17．交强险是车主必须为机动车购买的险种．若普通6座以下私家车投保交强险第一年的费用（基准保费）统一为a元，在下一年续保时，实行的是费率浮动机制，保费与上一年度车辆发生道路交通事故的情况相联系，发生交通事故的次数越多，费率也就越高，具体浮动情况如表：

交强险浮动因素和浮动费率比率表
	浮动因素	浮动比率
A1	上一个年度未发生有责任道路交通事故	下浮10%
A2	上两个年度未发生有责任道路交通事故	下浮20%
A3	上三个及以上年度未发生有责任道路交通事故	下浮30%
A4	上一个年度发生一次有责任不涉及死亡的道路交通事故	0%
A5	上一个年度发生两次及两次以上有责任道路交通事故	上浮10%
A6	上一个年度发生有责任道路交通死亡事故	上浮30%

某机构为了研究某一品牌普通6座以下私家车的投保情况，随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况，统计得到了下面的表格：

类型	A1	A2	A3	A4	A5	A6
数量	10	5	5	20	15	5

以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率，完成下列问题：
（Ⅰ）按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定a=950．记X为某同学家的一辆该品牌车在第四年续保时的费用，求X的分布列与数学期望值；（数学期望值保留到个位数字）
（Ⅱ）某二手车销售商专门销售这一品牌的二手车，且将下一年的交强险保费高于基本保费的车辆记为事故车．假设购进一辆事故车亏损5000元，一辆非事故车盈利10000元：
①若该销售商购进三辆（车龄已满三年）该品牌二手车，求这三辆车中至多有一辆事故车的概率；
②若该销售商一次购进100辆（车龄已满三年）该品牌二手车，求他获得利润的期望值．

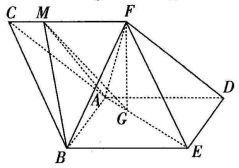16．如图，三棱柱ABC-DEF中，侧面ABED是边长为2的菱形，且∠ABE=$\frac{π}{3}$，BC=$\frac{\sqrt{21}}{2}$，四棱锥F-ABED的体积为2，点F在平面ABED内的正投影为G，且G在AE上，点M是在线段CF上，且CM=$\frac{1}{4}$CF．
（Ⅰ）证明：直线GM∥平面DEF；
（Ⅱ）求二面角M-AB-F的余弦值．

15．已知等差数列{a_n}的前n项和为S_n，若S_m-1=-4，S_m=0，S_m+2=14（m≥2，且m∈N^*）
（Ⅰ）求m的值；
（Ⅱ）若数列{b_n}满足$\frac{{a}_{n}}{2}$=log₂b_n（n∈N⁺），求数列{（a_n+6）•b_n}的前n项和．

14．在平面内将点A（2，1）绕原点按逆时针方向旋转$\frac{3π}{4}$，得到点B，则点B的坐标为（-$\frac{3\sqrt{2}}{2}$，$\frac{\sqrt{2}}{2}$）．

13．李冶（1192-1279），真定栾城（今属河北石家庄市）人，金元时期的数学家、诗人、晚年在封龙山隐居讲学，数学著作多部，其中《益古演段》主要研究平面图形问题：求圆的直径，正方形的边长等，其中一问：现有正方形方田一块，内部有一个圆形水池，其中水池的边缘与方田四边之间的面积为13.75亩，若方田的四边到水池的最近距离均为二十步，则圆池直径和方田的边长分别是（注：240平方步为1亩，圆周率按3近似计算）（　　）

A．

10步、50步

B．

20步、60步

C．

30步、70步

D．

40步、80步

12．设U=R，A={-3，-2，-1，0，1，2}，B={x|x≥1}，则A∩∁_UB=（　　）

A．

{1，2}

B．

{-1，0，1，2}

C．

{-3，-2，-1，0}

D．

{2}

11．设二面角α-CD-β的大小为45°，A点在平面α内，B点在CD上，且∠ABC=45°，则AB与平面β所成角的大小为30°．

10．设△ABC的内角A、B、C的对边分别为a、b、c，且满足sinA+sinB=[cosA-cos（π-B）]•sinC．
（1）试判断△ABC的形状，并说明理由；
（2）若a+b+c=1+$\sqrt{2}$，试求△ABC面积的最大值．

9．已知边长为2的正方形ABCD的四个顶点在球O的球面上，球O的体积为V_球=$\frac{160\sqrt{5}π}{3}$，则OA与平面ABCD所成的角的余弦值为$\frac{\sqrt{10}}{10}$．