练习册

  • 练习册
  • 试题
    相关习题
     0  237239  237247  237253  237257  237263  237265  237269  237275  237277  237283  237289  237293  237295  237299  237305  237307  237313  237317  237319  237323  237325  237329  237331  237333  237334  237335  237337  237338  237339  237341  237343  237347  237349  237353  237355  237359  237365  237367  237373  237377  237379  237383  237389  237395  237397  237403  237407  237409  237415  237419  237425  237433  266669 

    科目： 来源： 题型：解答题

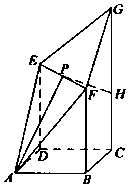    13．如图，四边形ABCD是边长为$\sqrt{2}$的正方形，CG⊥平面ABCD，DE∥BF∥CG，DE=BF=$\frac{3}{5}$CG．P为线段EF的中点，AP与平面ABCD所成角为60°．在线段CG上取一点H，使得GH=$\frac{3}{5}$CG．
    （1）求证：PH⊥平面AEF；
    （2）求二面角A-EF-G的余弦值．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    12．已知球的直径SC=6，A、B是该球球面上的两点，且AB=SA=SB=3，则棱锥S-ABC的体积为（　　）
    A．$\frac{{3\sqrt{2}}}{4}$B．$\frac{{9\sqrt{2}}}{4}$C．$\frac{{3\sqrt{2}}}{2}$D．$\frac{{9\sqrt{2}}}{2}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    11．已知平面向量$\overrightarrow{a}$=（1，m），$\overrightarrow{b}$=（2，5），$\overrightarrow{c}$=（m，3），且（$\overrightarrow{a}$+$\overrightarrow{c}$）∥（$\overrightarrow{a}$-$\overrightarrow{b}$），则m=（　　）
    A．$\frac{{-3+\sqrt{17}}}{2}$B．$\frac{{3-\sqrt{17}}}{2}$C．$\frac{{-3±\sqrt{17}}}{2}$D．$\frac{{3±\sqrt{17}}}{2}$

    查看答案和解析>>

    科目： 来源： 题型：填空题

    10．已知数列{an}的首项a1=2，数列{bn}为等比数列，且bn=$\frac{{a}_{n+1}}{{a}_{n}}$，又b10b11=2017${\;}^{\frac{1}{10}}$，则a21=4034．

    查看答案和解析>>

    科目： 来源： 题型：选择题

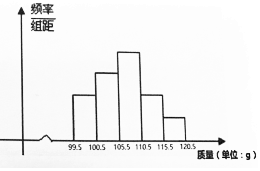    9．检测600个某产品的质量（单位：g），得到的直方图中，前三组的长方形的高度成等差数列，后三组对应的长方形的高度成公比为0.5的等比数列，已知检测的质量在100.5-105.5之间的产品数为150，则质量在115.5-120.5的长方形高度为（　　）
    A．$\frac{1}{12}$B．$\frac{1}{30}$C．$\frac{1}{6}$D．$\frac{1}{60}$

    查看答案和解析>>

    科目： 来源： 题型：填空题

    8．已知椭圆C：$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1，点M与C的焦点不重合，若M关于C的焦点的对称点分别为A，B，点M关于椭圆C上任意一动点的对称点为N，则|AN|+|BN|=20．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    7．某市需对某环城快速车道进行限速，为了调研该道路车速情况，于某个时段随机对100辆车的速度进行取样，测量的车速制成如下条形图：

    经计算：样本的平均值μ=85，标准差σ=2.2，以频率值作为概率的估计值．已知车速过慢与过快都被认为是需矫正速度，现规定车速小于μ-3σ或车速大于μ+2σ是需矫正速度．
    （1）从该快速车道上所有车辆中任取1个，求该车辆是需矫正速度的概率；
    （2）从样本中任取2个车辆，求这2个车辆均是需矫正速度的概率；
    （3）从该快速车道上所有车辆中任取2个，记其中是需矫正速度的个数为ε，求ε的分布列和数学期望．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    6．给出以下命题：
    （1）“0＜t＜1”是“曲线$\frac{x^2}{t}+\frac{y^2}{1-t}=1$表示椭圆”的充要条件
    （2）命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”
    （3）Rt△ABC中，|AC|=2，∠B=90°，∠C=30°．D是斜边AC上的点，|CD|=|CB|．以B为起点任作一条射线BE交AC于E点，则E点落在线段CD上的概率是$\frac{{\sqrt{3}}}{2}$
    （4）设随机变量ξ服从正态分布N（0，1），若P（ξ＞1）=0.2，则P（-1＜ξ＜0）=0.6
    则正确命题有（　　）个．
    A．0B．1C．2D．3

    查看答案和解析>>

    科目： 来源： 题型：选择题

    5．执行如图程序，输出S的值为（　　）
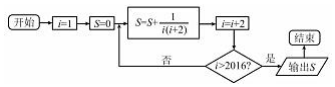
    A．$\frac{1007}{2015}$B．$\frac{1008}{2017}$C．$\frac{2016}{2017}$D．$\frac{2015}{4032}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    4．已知z=（m-3）+（m+1）i在复平面内对应的点在第二象限，则实数m的取值范围是（　　）
    A．（-3，1）B．（-1，3）C．（1，+∞）D．（-∞，-3）

    查看答案和解析>>

    同步练习册答案