13．执行如图所示的程序框图，如果输入的m=168，n=112，则输出的k，m的值分别为（　　）

A．

4，7

B．

4，56

C．

3，7

D．

3，56

12．某校为提高学生身体素质决定对全校高三900名学生，分三批次进行身体素质测试，在三个批次中男、女学生数如下表所示，已知在全体学生中随机抽取1名，抽到第二批次中女学生的概率是0.16．

	第一批次	第二批次	第三批次
女同学	196	x	y
男同学	204	156	z

（Ⅰ）求x的值；
（Ⅱ）已知y≥96，z≥96，求第三批次中女同学比男同学多的概率．

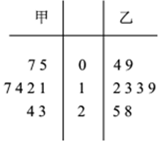11．如图是甲、乙两个商场统计同一时间段各自每天的销售额（单位：万元）的茎叶图，假设销售额的中位数为m，平均值为$\overline{x}$，则下列正确的是（　　）

	A．	m甲=m乙，$\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$		B．	m甲=m乙，$\overline{{x}_{甲}}$＜$\overline{{x}_{乙}}$
	C．	m甲＞m乙，$\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$		D．	m甲＜m乙，$\overline{{x}_{甲}}$＜$\overline{{x}_{乙}}$

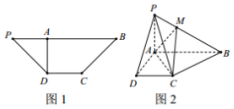10．如图1，在等腰梯形PDCB中，PB∥DC，PB=3，DC=1，∠DPB=45°，DA⊥PB于点A，将△PAD沿AD折起，构成如图2所示的四棱锥P-ABCD，点M的棱PB上，且PM=$\frac{1}{2}$MB．
（1）求证：PD||平面MAC；
（2）若平面PAD⊥平面ABCD，求二面角M-AC-B的余弦值．

9．从集合M={（x，y）|（|x|-1）²+（|y|-1）²＜4，x，y∈Z}中随机取一个点P（x，y），若xy≥k（k＞0）的斜率为$\frac{6}{25}$，则k的最大值是2．

8．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$夹角为60°，且|$\overrightarrow{a}$|=2，|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2$\sqrt{7}$，则|$\overrightarrow{b}$|=3．

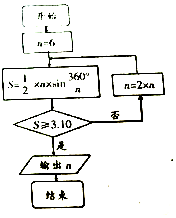7．如图是利用我国古代数学家刘徽的割圆术设计的程序框图，则输出的n值为（　　）
参考数据：$\sqrt{3}$≈1.732，sin15°≈0.2588，sin7.5°≈0.1305．

A．

12

B．

24

C．

48

D．

96

6．（x²+3x-y）⁵的展开式中，x⁵y²的系数为（　　）

A．

-90

B．

-30

C．

30

D．

90

5．某市为鼓励居民节约用水，将实行阶梯式计量水价，该市每户居民每月用水量划分为三档，水价实行分档递增．
第一级水量：用水量不超过20吨，水价标准为1.60元/吨；
第二级水量：用水量超过20吨但不超过40吨，超出第一级水量的部分，水价标准比第一级水价提高0.8元/吨；
第三级水量：用水量超过40吨，超出第二级水量的部分，水价标准比第一级水价提高1.60元/吨．
随机调查了该市500户居民，获得了他们某月的用水量数据，整理得到如下的频率分布表：

用水量（吨）	[0，10]	（10，20]	（20，30]	（30，40]	（40，50]	合计
频数	50	200	100	b	50	500
频率	0.1	a	0.2	c	0.1	1

（1）根据频率分布表中的数据，写出a，b，c的值；
（2）从该市调查的500户居民中随机抽取一户居民，求该户居民用水量不超过36吨的概率；
（3）假设同组中的每个数据用该组区间的中点值代替，试估计该市每户居民该月的平均水费．

4．如图，菱形ABCD的边长为12，∠BAD=60°，AC∩BD=O，将菱形ABCD沿对角线AC折起，得到三棱锥B-ACD，点M是棱BC的中点，DM=6$\sqrt{2}$．

（1）求证：OD⊥平面ABC；
（2）求三棱锥M-ABD的体积．